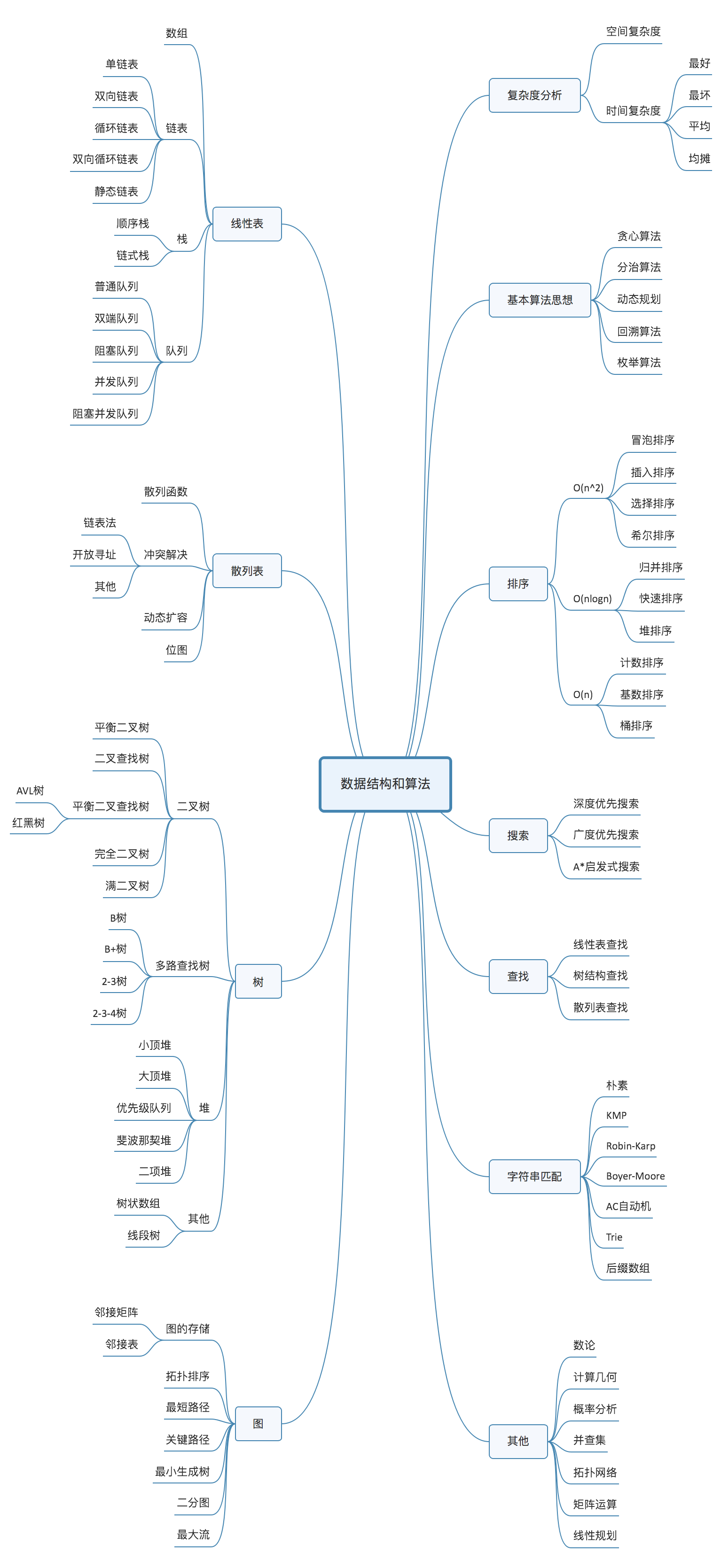
无论什么难题,降低复杂度的方法就是这三个步骤。只要你能深入理解这里的核心思想,就能把问题迎刃而解。
第一步,暴力解法。在没有任何时间、空间约束下,完成代码任务的开发。
第二步,无效操作处理。将代码中的无效计算、无效存储剔除,降低时间或空间复杂度。
第三步,时空转换。设计合理数据结构,完成时间复杂度向空间复杂度的转移。
既然说这是这门专栏的总纲,那么很显然后续的学习都是在这个总纲体系的框架中。第一步的暴力解法没有太多的套路,只要围绕你面临的问题出发,大胆发挥想象去尝试解决即可。第二步的无效操作处理中,你需要学会并掌握递归、二分法、排序算法、动态规划等常用的算法思维。第三步的时空转换,你需要对数据的操作进行细分,全面掌握常见数据结构的基础知识。再围绕问题,有针对性的设计数据结构、采用合理的算法思维,去不断完成时空转移,降低时间复杂度。
https://github.com/labuladong/fucking-algorithm
复杂度
消耗计算时间和计算空间
时间复杂度
- 对数阶
1
2
3
4
| int count =1;
while(count < n){
count = count * 2;
}
|
代码看到 2 * 2 * 2 … 最终离n很近,最终退出循环,2^x =n ,得到 x = log2^n,所以这个循环时间复杂度为O(logn)
空间复杂度
空间方面主要体现在计算过程中,对于存储资源的消耗情况


链表
p,q指向的都是整体
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| typedef struct node{
int data;
struct node *pNext;
} NODE, *PNODE;
PNODE p = (PNODE)malloc(sizeof(NODE));
free(p)
p->pNext;
|
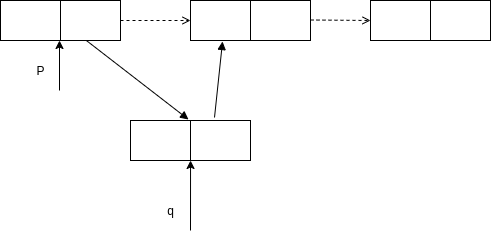
插入q节点
1
2
3
4
5
| 方法1:
r = p-> pNext ; p->pNext =q ; q->pNext = r;
方法2:
q->pNext = p->pNext;
p->pNext = q;
|
删除p后面的节点
1
2
3
| r = p->pNext;
p->pNext= r->pNext;
free(r);
|
双向链表
插入

1
2
3
4
5
6
| ListNodePosi <T> insertAsPred(T const&e){
ListNodePosi<T> x = new ListNode(e,pred,this);
pred->succ = x;
this->pred= x;
return x;
}
|
递归
- 递归必须得有一个明确的中止条件。
- 该函数所处理的数据规模必须在递减。
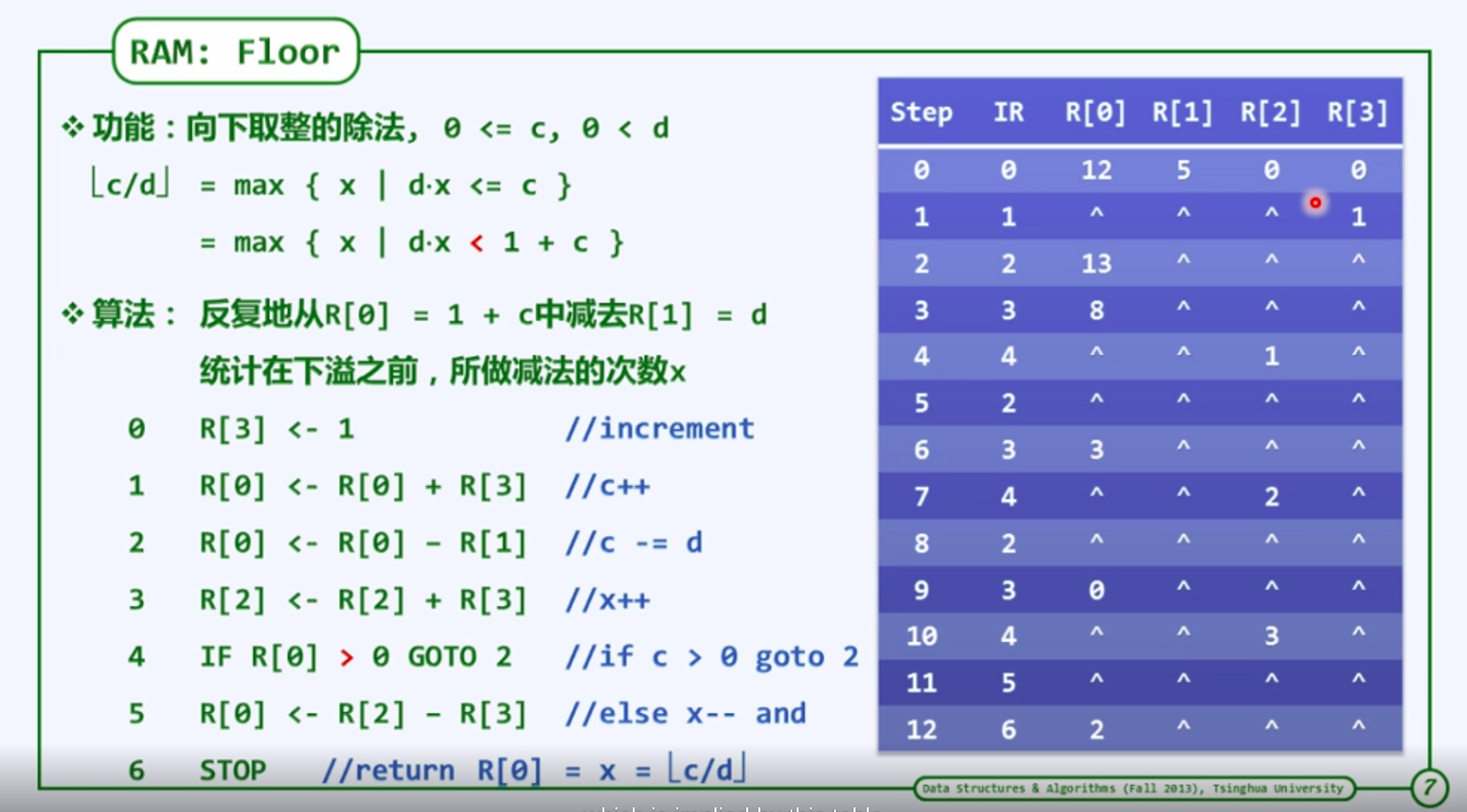
递归复杂度
递归跟踪(recursion trace)分析
1
2
3
4
| sum(int A[],int n){
return (n<1)?
0:sum(A,n-1)+A[n-1]
}
|
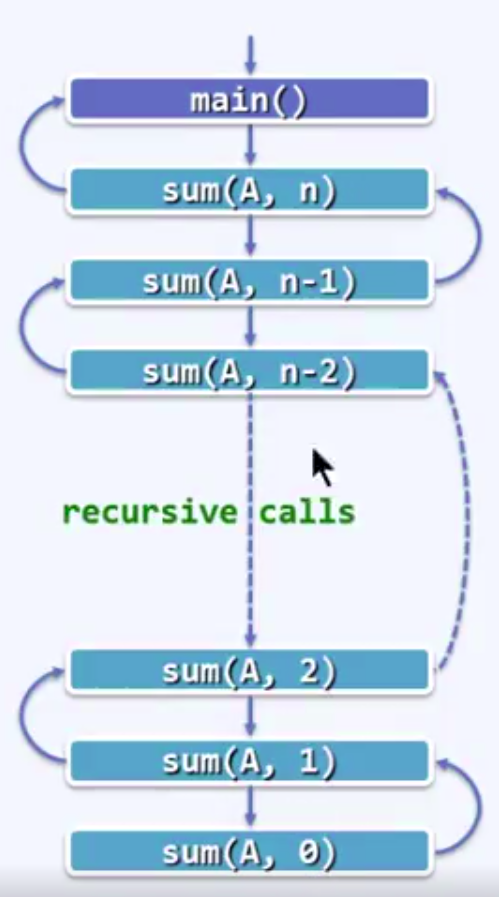
检查每个递归实例,累计所需的时间(调用语句本身,计入对应的子实例)
其总和即算法执行时间
本例中,单个递归实例自身只需o(1)时间
T(n) = o(1) * (n+1) = o(n)
递归方程
求解sum(A,n) : 递归求解规模为n-1的问题sum(A,n-1) 加上 A[n-1] 。
T(n) = T(n-1) + o(1) // 为了求解T(n)所需要的时间,花了T(n-1)的时间求解n-1的问题,然后再花了o(1)的时间
T(0) = o(1)
T(n) = T(n-1) + o(1) //两边同时 -n
T(n) -n = T(n-1) -(n-1)
= …
=T(2) - 2
= T(1) -1
=T(0)
T(n) = o(1) +n = o(n)
递归实例
阶乘 、求和
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| #include <stdio.h>
long f(int n);
long sum(int n);
int main(void) {
printf("n=1 输出 %ld \n ", f(1));
printf("n=2 输出 %ld \n ", f(2));
printf("n=3 输出 %ld \n ", f(3));
printf("n=4 输出 %ld \n ", f(4));
printf("n=5 输出 %ld \n ", f(5));
printf("n=100 相加 %ld \n ", sum(100));
int val,mult = 1;
printf("请输入一个数: val=");
scanf("%d",&val);
for (int i = 1; i <= val; ++i) {
mult = mult * i;
}
printf("%d的阶乘是: %d\n",val,mult);
}
long f(int n) {
if (n == 1) {
return 1;
} else {
return n * f(n - 1);
}
}
long sum(int n) {
if (n == 1) {
return 1;
} else {
return (n + sum(n-1));
}
}
|
汉诺塔
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| #include <stdio.h>
void hannuota(int n, char a, char b, char c) {
if (1 == n) {
printf("将编号为%d的盘子直接从%c柱子移到%c柱子\n", n, a, c);
} else {
hannuota(n - 1, a, c, b);
printf("将编号为%d的盘子直接从%c柱子移到%c柱子\n", n, a, c);
hannuota(n - 1, b, a, c);
}
}
int main(void) {
char ch1 = 'A';
char ch2 = 'B';
char ch3 = 'C';
printf("请输入要移动盘子的个数:");
int n;
scanf("%d",&n);
hannuota(n,'A','B','C');
return 0;
}
|
Fibonacci.c
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| #include <stdio.h>
#include <stdbool.h>
int f(int n){
if(n==0){
return 0;
} else if(n==1){
return 1;
} else{
return f(n-1)+f(n-2);
}
}
int main(){
int n;
printf("输入n的值为 ");
while (true){
scanf("%d",&n);
printf("f(n) %d \n",f(n));
}
}
|
上面这种求和方式,随着n增加,时间复杂度会指数型增加,到了40已经算不动了,里面会有大量重复的计算
1
2
3
4
5
6
7
8
9
| int f(int n) {
int f = 0;
int g = 1;
while (n--){
g = g+f;
f = g-f;
}
return g;
}
|
这种时间复杂度O(n),不要太快,交替滚动向前推进。
Hash(散列)
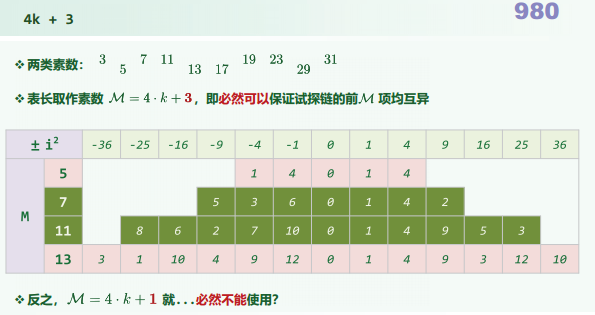
[Hash(key) + 1^2] % M 以平方数为距离,确定下一试探桶单元
M为三列表的容量