LC-Tree-Search-22

二叉树搜索 BST

根节点比左子树所有节点的数值都大，比右子树所有节点的数值都小.

700. 二叉搜索树中的搜索

My idea

DFS

  1. 先序遍历搜索，如果找到了直接返回当前节点。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    fun searchBST(root: TreeNode?, `val`: Int): TreeNode? {
        if (root == null) return null
        if (root.`val` == `val`) {
            return root
        }
        val nodeLeft = searchBST(root.left, `val`)
        if (nodeLeft != null) {
            return nodeLeft
        }
        val nodeRight = searchBST(root.right, `val`)
        if (nodeRight != null) {
            return nodeRight
        }
        return null
    }

看了官方解法,利用二叉搜索树的特性 

1
2
3
4
5
6
7
8
9
10
11
fun searchBST1(root: TreeNode?, `val`: Int): TreeNode? {
    if (root == null) return null
    var node: TreeNode? = root.left
    if (root.`val` == `val`) { //一开始没有做出来，这个条件没写,导致一直往下递归
        return root
    }
    if (root.`val` < `val`) {
        node = root.right
    }
    return searchBST1(node, `val`)
}
迭代法

二叉搜索树的迭代法相对简单，暂时先不看了

98. 验证二叉搜索树

二叉搜索树是一个有序树：

  • 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 注意==都不行
  • 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
  • 它的左、右子树也分别为二叉搜索树

这就决定了，二叉搜索树，递归遍历和迭代遍历和普通二叉树都不一样。

一开始理解错了，只比较根节点和左右子树，导致下面这个testcase没通过，应该是根节点和所有的左右子树的节点数组

1
5, 4, 6, null, null, 3, 7
转数组

把中序遍历转成数组很好理解

  1. 中序遍历递归 得到list数组

  2. 比较数组的前后节点大大小,

  3. 如果前面节点值更大，那么直接返回false, ==也不行

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
val list = LinkedList<Int>()
fun isValidBST3(root: TreeNode?): Boolean {
    dfsTraversal(root) // 中序遍历递归 得到list数组
    for (i in 0 until list.size - 1) { // 比较数组的前后节点大大小
        if (list[i] >= list[i + 1]) { // 如果前面节点值更大，那么直接返回false, ==也不行
            return false
        }
    }
    return true
}

private fun dfsTraversal(root: TreeNode?) {
    if (root == null) return
    dfsTraversal(root.left)
    list.add(root.`val`)
    dfsTraversal(root.right)
}
递归解法

随想录的递归解法，一开始怎么也理解不了，其实和上面 中序转数组的类似，就是把根据中序遍历遍历的节点，后一个节点一定比前一个节点的数值高。

  1. 中序遍历 后一个节点比前一个节点的值大，就可以了，所以存储前一个节点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
var preNode: TreeNode? = null
fun isValidBST4(root: TreeNode?): Boolean {
    if (root == null) return true
    if (!isValidBST4(root.left)) {
        return false
    }
    if (preNode != null && preNode!!.`val` >= root.`val`) {
        return false
    }
    preNode = root
    if (!isValidBST4(root.right)) {
        return false
    }
    return true
}

之前的题主要用到 后序和先序，二叉搜索这里开始用到了 中序遍历。

530. 二叉搜索树的最小绝对差

My idea

这一题和上一题 98 思路差不多，

中序遍历的节点之间的数组相差最小，所以找出节点间的间隔最小值就可以了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
var preNode: TreeNode? = null
var miniNum = Int.MAX_VALUE
fun getMinimumDifference(root: TreeNode?): Int {
    if (root == null) return Int.MAX_VALUE
    getMinimumDifference(root.left)
    if (preNode != null) {
        val gapNum = root.`val` - preNode!!.`val`//这一步可以简化 Math.min()
        if (gapNum < miniNum) {
            miniNum = gapNum
        }
    }
    preNode = root
    getMinimumDifference(root.right)
    return miniNum
}

也可以先中序遍历转成数组，然后求数组元素间的差值就可以了。

501. 二叉搜索树中的众数

My idea

我的想法和上面的类似。

  1. 中序遍历相邻节点用map存下value和值的个数。
  2. 遍历map求得最大个事的数组。把map按照value个数进行数组排序
  3. 然后取排序后的前面的元素

。了。/其实上面这种方式，用先序 后序都可以，都不需要二叉搜索树。

其实上面我的想法也是 打算用二叉搜索树的特性，放到map中，然后把map排序,就不知道怎么处理更好。看了随想录的处理方式,理了下思路.

  1. 根据中序遍历的前后节点，他们的值相同的是一起的，进行遍历。
  2. 对value值进行count计数，如果count == 最大个数，加入集合。
  3. 如果count>最大个数，清空集合.

一开始不知道放哪里, maxCount=count ，以为在前面if (preNode != null && preNode!!.val == node.val) 前面的比较里面,还想着Math.max,但是都不合适。然后看了一半随想录是放在更新节点的位置，更好.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
val array = ArrayList<Int>()
fun findMode(root: TreeNode?): IntArray {
    inDFS(root)
    return array.toIntArray()
}

var preNode: TreeNode? = null
var maxCount = 0
var count = 0
private fun inDFS(node: TreeNode?) {
    val printNode = node?.`val`
    println("printNode $printNode")
    if (node == null) {
        return
    }
    inDFS(node.left)
    if (preNode != null && preNode!!.`val` == node.`val`) {
        count++
    } else {
        count = 1
    }
    if (count == maxCount) {
        array.add(node.`val`)
    }
    if (count > maxCount) {
        maxCount = count//这一步一开始不知道放哪里,看了一眼随想录答案
        array.clear() // 有更大的值，清空之前的集合
        array.add(node.`val`)
    }
    preNode = node
    inDFS(node.right)
}

官方还有 o(1)的处理，while循环

https://leetcode.cn/problems/find-mode-in-binary-search-tree/solution/er-cha-sou-suo-shu-zhong-de-zhong-shu-by-leetcode-/

236. 二叉树的最近公共祖先

这一题有两种想法

  1. 之前做的环形链表 走对方的路
  2. 先序遍历每一个节点，只要下面的节点都走过，只要下一个节点没有走到，就返回上一个节点，但是先序遍历DFS 两个节点都走了不知道怎么返回。

看了随想录视频思路后 https://www.bilibili.com/video/BV1jd4y1B7E2

  1. 后序遍历如果碰到p或q,就返回他们的节点.
  2. 如果一个节点的左右子树都不为空说明当前节点是他们的最近公共祖先.
  3. 还一种情况，有一个节点p就是祖先节点

debug调试，拼凑把代码写出来了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
    fun lowestCommonAncestor(root: TreeNode?, p: TreeNode?, q: TreeNode?): TreeNode? {
        if (root == null) return null // 随想录这里改成 碰到节点判断，直接在这里返回
//        val printData = root.`val`
//        println(printData)
        val leftNode = lowestCommonAncestor(root.left, p, q)
        val rightNode = lowestCommonAncestor(root.right, p, q)
        if (leftNode != null && rightNode != null) { // 如果左右子树都不为空，那么当前节点就是最近公共祖先节点
            return root
        }
        if (p != null && root.`val` == p.`val`) {   //碰到了其中一个节点返回
            return root
        } else if (q != null && root.`val` == q.`val`) {
            return root                             //碰到了其中一个节点返回
        }
        if (leftNode != null) return leftNode       //回溯之前碰到的节点
        if (rightNode != null) return rightNode
        return null
    }
终止条件写法

随想录这里改成 碰到节点判断，直接在这里返回，下次可以改成在终止条件这里，更简单

235. 二叉搜索树的最近公共祖先

My idea

可以根据二叉搜索树的特性， 祖先节点的值大小有两种情况

  1. 在p和q之前,
  2. 如果p<q, 祖先节点的值 等于p , 大于q
  3. 只要满足上述条件，用先序遍历或者后序遍历都可以，把节点返回

官方和随想录解法都是给出了相反的条件 ，当前节点<p , >q,在外面的情况（其实这里没想清楚,不存在这样的<2 >4的节点）, 但是我这里ide testcase也没问题。

https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-search-tree/solution/er-cha-sou-suo-shu-de-zui-jin-gong-gong-zu-xian-26/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/**
 * 很奇怪，IDE可以跑这个testcase没问题
 *[2,1]
 * 2
 * 1
 */
fun lowestCommonAncestor(root: TreeNode?, p: TreeNode?, q: TreeNode?): TreeNode? {
    if (root == null) return null
    if (p!!.`val` > q!!.`val`) {
        swap(p, q)
    }
    if (root.`val` > p.`val` && root.`val` < q.`val`) { 
        return root
    }
    if (root.`val` == p.`val` && root.`val` < q.`val`) {
        return root
    }
    if (root.`val` == q.`val` && root.`val` > p.`val`) {
        return root
    }
    val leftNode = lowestCommonAncestor(root.left, p, q)
    if (leftNode != null) return leftNode
    val rightNode = lowestCommonAncestor(root.right, p, q)
    if (rightNode != null) return rightNode
    return null
}

fun swap(p: TreeNode, q: TreeNode?) {
    val temp = p.`val`
    p.`val` = q!!.`val`
    q.`val` = temp
}

https://programmercarl.com/0235.%E4%BA%8C%E5%8F%89%E6%90%9C%E7%B4%A2%E6%A0%91%E7%9A%84%E6%9C%80%E8%BF%91%E5%85%AC%E5%85%B1%E7%A5%96%E5%85%88.html

https://www.bilibili.com/video/BV1Zt4y1F7ww

看了随想录视频，其实相反的就两种情况

  1. 当前节点 <p , <q， 那么p,q一定在右子树上，就去右子树去找
  2. 当前节点 > p , >q ,那么p,q一定在左子树上，就去左子树去找
1
2
3
4
5
6
7
8
9
10
11
12
13
fun lowestCommonAncestor(root: TreeNode?, p: TreeNode?, q: TreeNode?): TreeNode? {
    if (root == null) return null
    if (root.`val` < p!!.`val` && root.`val` < q!!.`val`) { // 当前节点比p和q的值都小，那么一定p,q一定在右子树上，就往右边遍历
        val rightNode = lowestCommonAncestor(root.right, p, q)
        if (rightNode != null) return rightNode
    }

    if (root.`val` > p.`val` && root.`val` > q!!.`val`) {
        val leftNode = lowestCommonAncestor(root.left, p, q)
        if (leftNode != null) return leftNode
    }
    return root
}

701. 二叉搜索树中的插入操作

DFS

My idea

可以用后序遍历，按照二叉树的特性，走到叶子节点后，连接到叶子节点，然后回溯到根节点并返回

  1. 后序遍历根据待插入值和当前节点比较，找到需要插入的位置。
  2. 如果需要插入的位置左或右节点刚好为空，就插入。

随想录其中一个解法和我的这个类似，不过感觉比我这个更复杂点

自己的做的解法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
fun insertIntoBST(root: TreeNode?, `val`: Int): TreeNode? {
    if (root == null) return TreeNode(`val`) //有一个这个test case  [] 5 ,空树的话返回 [5]

    if (`val` < root.`val`) { // 插入点小于当前节点，往左子树中插入
        insertIntoBST(root.left, `val`)
    }
    if (`val` > root.`val`) {
        insertIntoBST(root.right, `val`)
    }
    // 一开始这个放前面导致添加了两个5的左节点，因为 insertIntoBST(root.left, `val`)又走了一次
    val treeNode = TreeNode(`val`) // 只有一次机会走这个
    if (root.right == null && `val` > root.`val`) { //  待插入点大于当前节点，所以要插入右子树中，此时右子树为空，那么直接插入
        root.right = treeNode
    } else if (root.left == null && `val` < root.`val`) {
        root.left = treeNode
    }
    return root
}

看了随想录的解法，其实还可以每一个都被父节点接住更简单,也是后序遍历的精髓 

1
2
3
4
5
6
7
8
9
10
11
12
fun insertIntoBST(root: TreeNode?, `val`: Int): TreeNode? {
    if (root == null) {
        return TreeNode(`val`)
    }
    if (`val` < root.`val`) { // 插入点小于当前节点，往左子树中插入
        root.left = insertIntoBST1(root.left, `val`)
    }
    if (`val` > root.`val`) {
        root.right = insertIntoBST1(root.right, `val`)
    }
    return root
}
迭代法

官方用迭代法 ,看起来也不难

https://leetcode.cn/problems/insert-into-a-binary-search-tree/solution/er-cha-sou-suo-shu-zhong-de-cha-ru-cao-zuo-by-le-3/

450. 删除二叉搜索树中的节点

My idea

和上面思路类似，用后序遍历的 父节点接住，当前要删除节点的左或者右节点，那么当前节点就删除了，然后左右节点再改变指向。

  1. 后序遍历到要删除的节点.

  2. 当前节点的右节点指向它的左节点。被上一个节点回溯的父节点接住。

  3. 返回当前节点的左节点，

[5,3,6,2,4,null,7]
5
优先还是需要右节点上去，否则就很麻烦，需要4上去

删除节点主要有这5种情况

  • 第一种情况：没找到删除的节点，遍历到空节点直接返回了
  • 找到删除的节点
    • 第二种情况：删除的左右孩子都为空（叶子节点），直接删除节点， 返回NULL为根节点
    • 第三种情况：删除节点的左孩子为空，右孩子不为空，删除节点，右孩子补位，返回右孩子为根节点
    • 第四种情况：删除节点的右孩子为空，左孩子不为空，删除节点，左孩子补位，返回左孩子为根节点
    • 第五种情况：删除节点的左右孩子节点都不为空，则将删除节点的左子树头结点（左孩子）放到删除节点的右子树的最左面节点的左孩子上，返回删除节点右孩子为新的根节点。

450.删除二叉搜索树中的节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
fun deleteNode(root: TreeNode?, key: Int): TreeNode? {
    if (root == null) return null //情况一
    if (key < root.`val`) {
        root.left = deleteNode(root.left, key)
    } else if (key > root.`val`) {
        root.right = deleteNode(root.right, key)
    }

    if (key == root.`val`) {
        if (root.right == null && root.left == null) {
            return null // 情况2  [0] 0 因为这个testcase 会返回[0]和预期不一致
        } else if (root.left != null && root.right == null) {            //情况三 如果左节点不为空
            val node = root.left  // 左节点 2 推到删除的节点位置
            if(root.right!=null){               //这两句可以去掉 ，直接返回节点
                node.right = root.right         //此时左节点2在在删除节点位置，它的右子树指向之前右节点4
            }
            return node
        } else if (root.right != null && root.left == null) {  //情况四 如果右节点不为空
            val node = root.right //右节点4 推到删除的节点位置
            if(root.left!=null){                 //这两句可以去掉
                node.left = root.left           // 此时左节点4在在删除节点位置，它的左子树指向之前右节点2
            }
            return node
        } else {
            val rightNode = root.right //情况五
            var leftNode = rightNode?.left
            while (leftNode?.left!= null) {
                leftNode = leftNode.left
            }
            if (leftNode != null) {
                leftNode.left = root.left
            } else {
                rightNode.left = root.left
            }
            root.left = null
            return rightNode // 这里返回的节点，可以被上面的左右子树接住
        }
    }
    return root
}
普通二叉树的节点删除

通用二叉树节点删除

要加if (leftNode != null)，否则删除报错

这个题目的leetcode的测试用例有问题,单独跑报错.

108. 将有序数组转换为二叉搜索树

看了随想录的解答，从中取中间节点的位置就可以了，如果数字是偶数，中间节点的两个中的一个都可以，

但是问题来了，为什么取中间节点构造的二叉树就是高度平衡的二叉搜索树呢?

先按照这个思路，把代码写出来

  1. 按照先序遍历思路，先找到根节点，构造出中间节点。
  2. 根据中间节点划定新的数组的范围，左边和右边，然后递归找到新的数组的中间节点继续划出范围.

在这里 左闭右闭更合理

这题主要注意边界值,if (left > right）这个要注意是> 没有=,因为index-1和index+1了，所以最终一定会超过right

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
fun sortedArrayToBST(nums: IntArray): TreeNode? {
    return buildSearchTree(nums, 0, nums.size - 1)
}

private fun buildSearchTree(nums: IntArray, left: Int, right: Int): TreeNode? {
    if (left > right) {
        return null
    }
    val index = /*(start + end) / 2*/ left + (right - left) / 2
    val node = TreeNode(nums[index])
    // println("node ${node.`val`} :  start $left end $right")
    node.left = buildSearchTree(nums, left, index - 1)
    node.right = buildSearchTree(nums, index + 1, right)
    return node
}

538. 把二叉搜索树转换为累加树

累加树: 按照中序遍历的到的 从小到大的数组 [1,2,3,4] ,累加树就是右到左的值相加 [10,9,7,4]

https://programmercarl.com/0538.%E6%8A%8A%E4%BA%8C%E5%8F%89%E6%90%9C%E7%B4%A2%E6%A0%91%E8%BD%AC%E6%8D%A2%E4%B8%BA%E7%B4%AF%E5%8A%A0%E6%A0%91.html#%E9%80%92%E5%BD%92

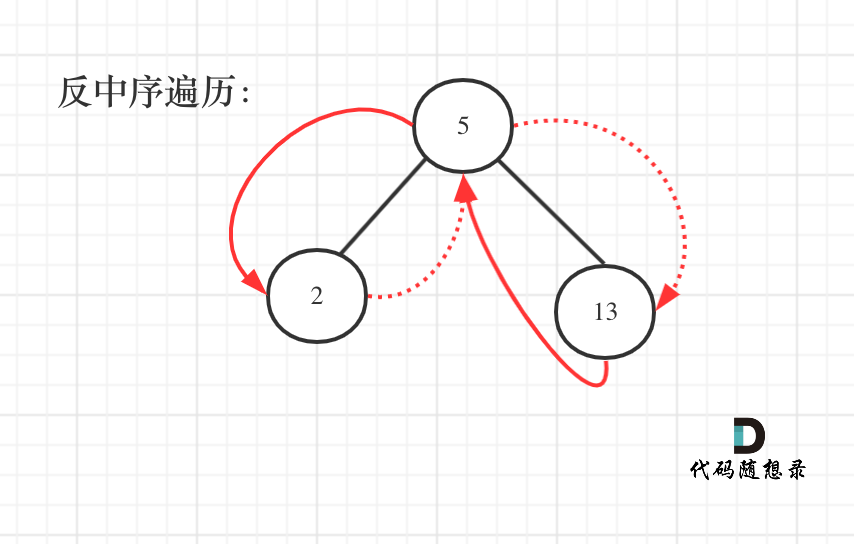
中序遍历的树 : 左 中 右 2 , 5, 13

反中序遍历的: 右 中 左 13 , 5 , 2

然后按照反中序遍历的到节点累加就可以了。

538.把二叉搜索树转换为累加树

这一题一开始没想上面的思路，看了随想录的思路后,写出来的

1
2
3
4
5
6
7
8
9
var sum = 0
fun convertBST(root: TreeNode?): TreeNode? {
    if (root == null) return null
    convertBST(root.right)
    sum += root.`val`
    root.`val` = sum
    convertBST(root.left)
    return root
}
  1. 根据中序遍历的规则，写出反中序 右中左遍历节点。
  2. 拿到每次中序的到的节点累加，然后赋值给当前节点。
sum += root.`val`
root.`val` = sum

这一段可以改进，可以保存前一个节点值，然后加上当前节点就可以了。

1
2
3
4
5
6
7
8
9
var pre = 0
fun convertBST1(root: TreeNode?): TreeNode? {
    if (root == null) return null
    convertBST(root.right)
    root.`val` += pre
    pre = root.`val`
    convertBST(root.left)
    return root
}
DataStructure
#LEETCODE
LC-Tree-Search-22
https://noteforme.github.io/2022/10/05/LC-Tree-Search-22/
Author
Jon
Posted on
October 5, 2022
Licensed under