LC-backtrack-combination

组合

组合的元素是无序的[1,2] , [2,1]是一个组合

组合的元素是不能重复的

77. 组合

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

https://www.bilibili.com/video/BV1ti4y1L7cv

拿到第一个元素.
用上面的图很形象,在剩余的元素中取数据，和二叉树路径很像,递归加回溯的过程.

这里一开始用的是 startIndex+1,不理解，这里回溯后,最第一次的for (i in startIndex..n)如果i ==2,或者3，或者4, 递归到底层，再回溯到第一次循环的时候，startIndex都是第一次的2,这样就导致剩余的元素不对

fun combine(n: Int, k: Int): List<List<Int>> {
    backTracking(n, k, 1)
    return result
}

private fun backTracking(n: Int, k: Int, startIndex: Int) {
    if (path.size == k) {
        result.add(path.toMutableList())
        return
    }
    for (i in startIndex..n) {
        path.add(i)
        backTracking(n, k, i + 1) // 这里一开始用的是 startIndex+1
        path.remove(i)
    }
}

组合剪枝

https://www.bilibili.com/video/BV1wi4y157er/

https://programmercarl.com/0077.%E7%BB%84%E5%90%88.html#%E5%89%AA%E6%9E%9D%E4%BC%98%E5%8C%96

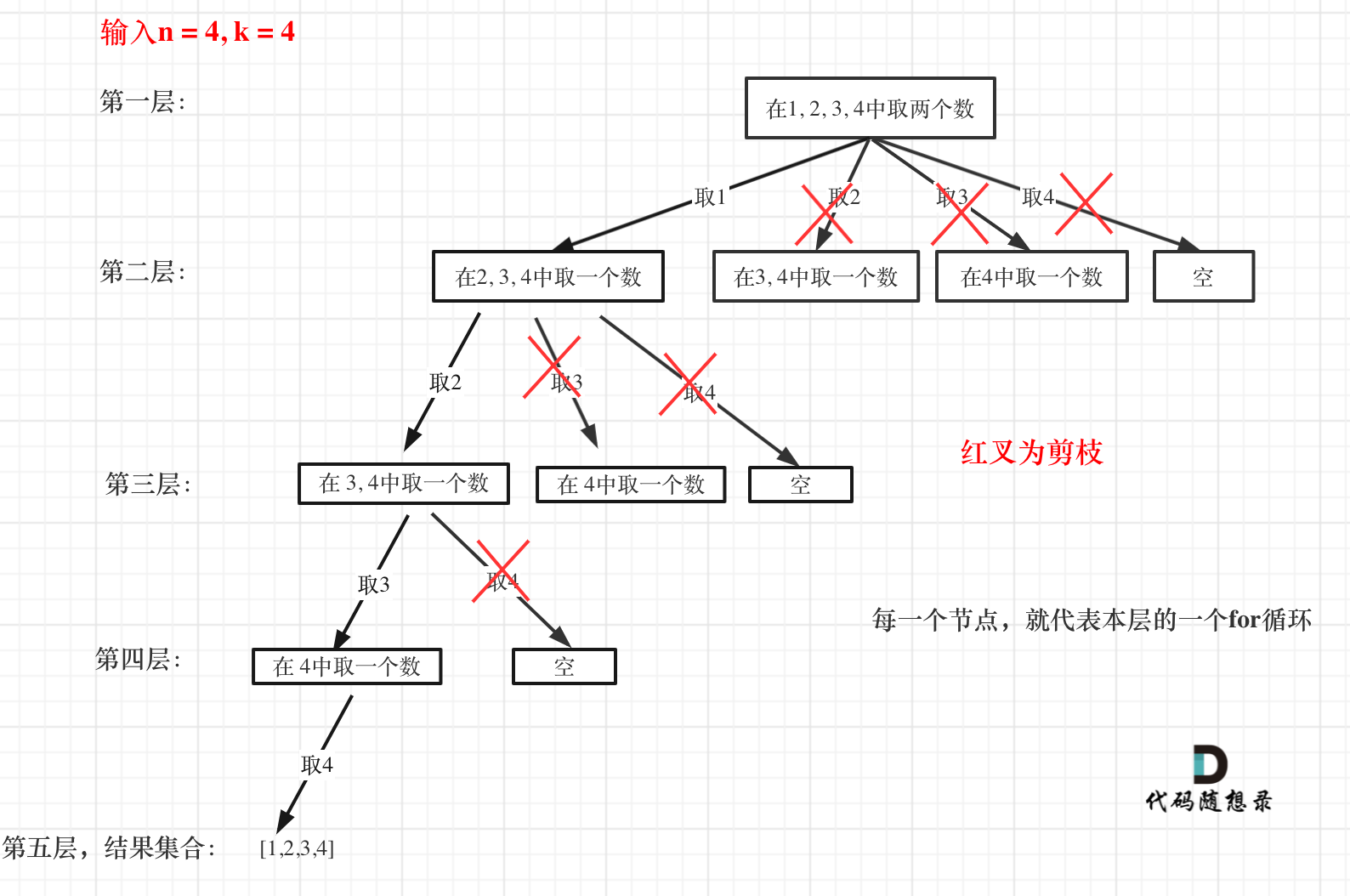
来举一个例子，n = 4，k = 4的话，那么第一层for循环的时候，从元素2开始的遍历都没有意义了。在第二层for循环，从元素3开始的遍历都没有意义了。

77.组合4

for (i in startIndex..n) { // 这里对应模拟就是,取1,取2 ,取3,取4 ,几个子孩子的操作.
         path.add(i)
         backTracking(n, k, i + 1) // 这里一开始用的是 startIndex+1
         path.remove(i)
}

剪枝就是 i< n这个范围里面做操作。

接下来看一下优化过程如下：

已经选择的元素个数：path.size();
还需要的元素个数为: k - path.size();
在集合n中至多要从该起始位置 : n - (k - path.size()) + 1，开始遍历

为什么有个+1呢，因为包括起始位置，我们要是一个左闭的集合。

举个例子，n = 4，k = 3，目前已经选取的元素为0（path.size为0），n - (k - 0) + 1 即 4 - ( 3 - 0) + 1 = 2。

从2开始搜索都是合理的，可以是组合[2, 3, 4]。

这里大家想不懂的话，建议也举一个例子，就知道是不是要+1了。

val path = ArrayList<Int>()
val result = ArrayList<List<Int>>()
fun combine(n: Int, k: Int): List<List<Int>> {
    backTracking1(n, k, 1)
    return result
}
//剪枝操作
private fun backTracking1(n: Int, k: Int, startIndex: Int) {
    if (path.size == k) {
        result.add(path.toMutableList())
        return
    }
    for (i in startIndex..(n - (k - path.size) + 1)) {
        path.add(i)
        backTracking1(n, k, i + 1) // 这里一开始用的是 startIndex+1
        path.remove(i)
    }
}

216. 组合总和 III

只使用数字1到9 .
每个数字 最多使用一次 .

从1开始选取，每次循环往后选取，如果往前选数字入[1,2], [2,1]的情况，就重复了.
选取元素综合==n , 并且是k个，装入数组。

我的解法if (sum == n && pathList.size == k)放一起不好，pathList.size到了k 个数，后面的就不用加了，达到竖向剪枝的目的。

private val result = ArrayList<List<Int>>()
private var sum: Int = 0 //集合的和
private val pathList = ArrayList<Int>() // 集合
fun combinationSum3(k: Int, n: Int): List<List<Int>> {
    blockTracking(k, n, 1)
    return result
}

private fun blockTracking(k: Int, n: Int, startIndex: Int) {
    if (sum == n && pathList.size == k) { // 相加之和为 n 的 k 个数的组合
        result.add(pathList.toMutableList())
        return
    }
    for (i in startIndex..9) {
        sum += i
        pathList.add(i)
        blockTracking(k, n, i + 1)
        sum -= i
        pathList.remove(i)
    }
}

剪枝

还没想好

216.组合总和III1

pathList.size到了k 个数，后面的就不用加了，达到竖向剪枝的目的。
(9 - (k - pathList.size) + 1) 分析

k - pathList.size : 从1开始选取,还差多少个元素

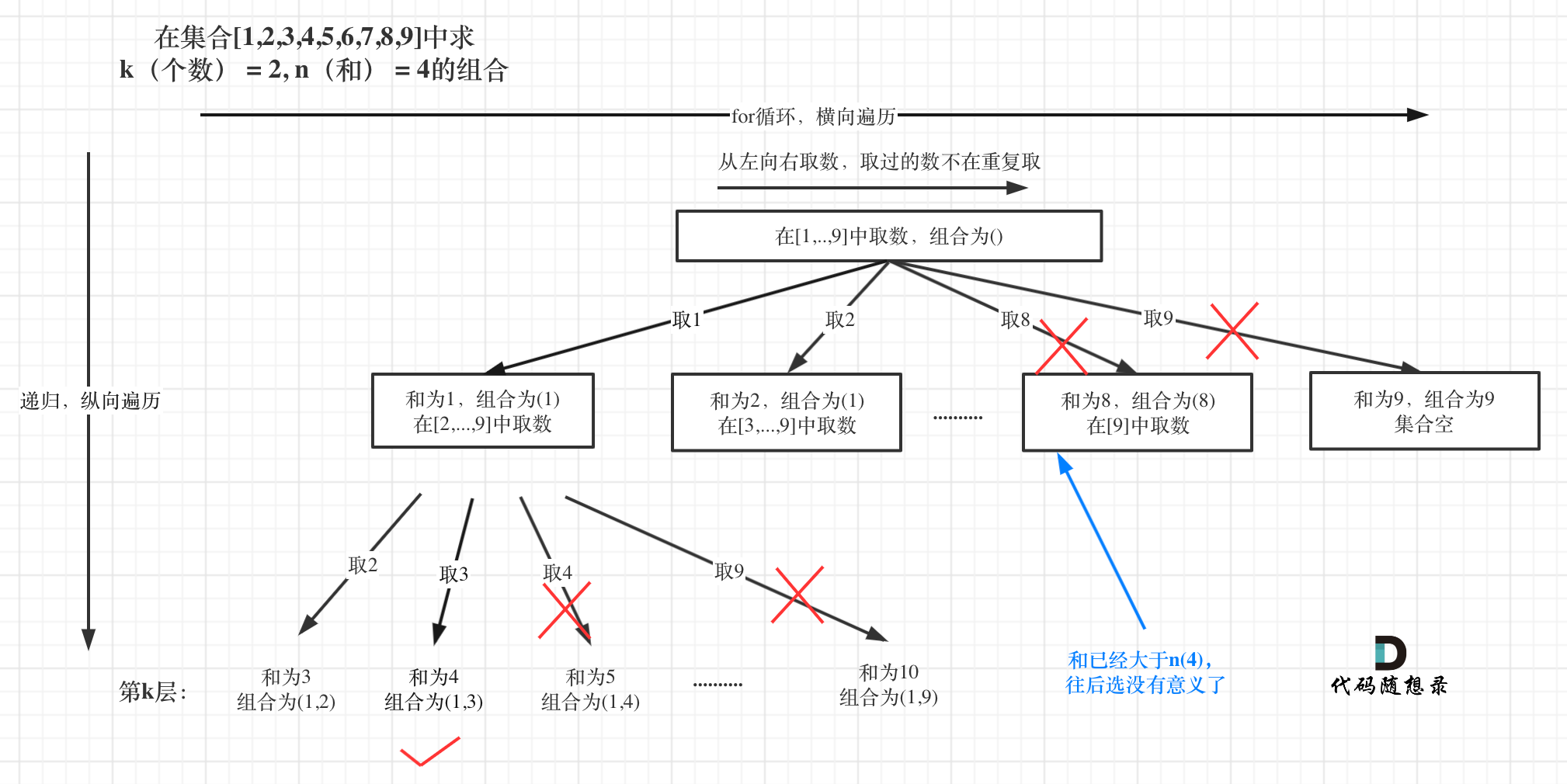
9 - (k - pathList.size) : 如果从1…9选取，为了避免重复，一直往大的数选取,第1次选到了8,如果k==2,那么过了8就没意义了，第一次的9就不需要选取了.

(9 - (k - pathList.size) + 1) 处理下标值。

private val result = ArrayList<List<Int>>()
private var sum: Int = 0 //集合的和
private val pathList = ArrayList<Int>() // 集合
fun combinationSum3(k: Int, n: Int): List<List<Int>> {
    blockTracking(k, n, 1)
    println(result)
    return result
}

private fun blockTracking(k: Int, n: Int, startIndex: Int) {
    if (pathList.size == k) { //shuxiang
        if (sum == n) {
            result.add(pathList.toMutableList())
        }
        return
    }
    for (i in startIndex..(9 - (k - pathList.size) + 1)) { // 横向剪枝
        if (sum > n) { //剪枝
            break
        }
        sum += i
        pathList.add(i)
        blockTracking(k, n, i + 1)
        sum -= i
        pathList.remove(i)
    }
}

private fun blockTracking(k: Int, n: Int, startIndex: Int) {
    if (sum > n) {
        return //sum > n 直接返回，随想录的解法，这样更好.
    }
    if (pathList.size == k) {
        if (sum == n) {
            result.add(pathList.toMutableList())
        }
        return
    }
    for (i in startIndex..(9 - (k - pathList.size) + 1)) {
        sum += i
        pathList.add(i)
        blockTracking(k, n, i + 1)
        sum -= i
        pathList.remove(i)
    }
}

17.电话号码的字母组合

前面的题目都是在一个数组里面取，看到这个问题，这个问题是在数组里面，再取里面的数组。

问题是，如果输入”235”,那么他们内部数组的索引startIndex怎么求出来.

String中的数字转int

val digits = "23"
val c = digits[0] - '0' // 50 - 48
println(digits[0].code) // ASCII是 50
println('0'.code)       //ASCII是 48

39.组合总和

这题目和前面的区别是，可以选取重复的元素.

选了2后，第二列选5这时候不能选2了，否则就会重复了。

看了随想录分析视频，在分析代码前，根据上面的图了解到的思路.

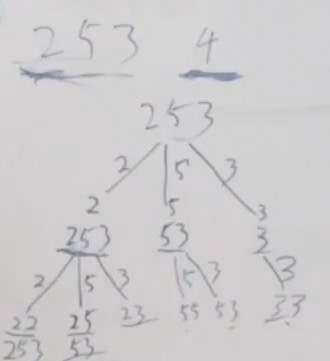
整体回溯架构和前面的都是一样的,选了2后，后面还是可以继续253, 选了5后只有53了，否则就有重复的。
一开始我的解法是backTrack(candidates.toList(), target,i),传入for循环中的i，这样会导致有漏掉前面的情况。要知道for循环的部分就是树的宽度。
后面的剪枝应该也是针对这部分。

var sum = 0
private val path = ArrayList<Int>()
private val result = ArrayList<List<Int>>()
fun combinationSum(candidates: IntArray, target: Int): List<List<Int>> {
    backTrack(candidates.toList(), target)
    return result
}

private fun backTrack(candidates: List<Int>, target: Int) {
    if (sum > target) {  // 节点和
        return
    }
    if (sum == target) { 
        result.add(path.toList())
        return
    }
    for ((i, item) in candidates.withIndex()) {
        path.add(item)
        sum += item
        backTrack(candidates.toMutableList().subList(i, candidates.size), target) // 只需要传入后面能选取的数组部分
        path.remove(item)
        sum -= item
    }
}

看了随想录的部分解法视频后，感觉这种更好，根据startIndex来取数组位置。传入startIndex后，后面的智能从startIndex后面取，和分割数组是一样的道理，感觉效率会更好。

var sum = 0
private val path = ArrayList<Int>()
private val result = ArrayList<List<Int>>()
fun combinationSum(candidates: IntArray, target: Int): List<List<Int>> {
    backTrack(candidates.toList(), target, 0)
    return result
}
private fun backTrack(candidates: List<Int>, target: Int, startIndex: Int) {
    if (sum > target) {
        return
    }
    if (sum == target) {
        result.add(path.toList())
        return
    }
    for (i in startIndex until candidates.size) {
        path.add(candidates[i])
        sum += candidates[i]
        backTrack(candidates, target, i) // i后分割元素，一开始写的是startIndex，这样for循环后面的就没过滤到了,只有startIndex过滤到了。
        path.remove(candidates[i])
        sum -= candidates[i]
    }
}

剪枝

如果target ==4

可以看这张图，如果经过排序左边的 235,取了2,3已经 >=4了，那么后面的5就不用去取了.

    var sum = 0
    private val path = ArrayList<Int>()
    private val result = ArrayList<List<Int>>()
    fun combinationSum(candidates: IntArray, target: Int): List<List<Int>> {
//        backTrack1(candidates.toList(), target)
        Arrays.sort(candidates) //剪枝前需要排序
        backTrack(candidates.toList(), target, 0)
        return result
    }
    private fun backTrack(candidates: List<Int>, target: Int, startIndex: Int) {
        if (sum > target) {
            return
        }
        if (sum == target) {
            result.add(path.toList())
            return
        }
        for (i in startIndex until candidates.size) {
            if (sum + candidates[i] > target) { //  剪枝操作
                return
            }
            path.add(candidates[i])
            sum += candidates[i]
            backTrack(candidates, target, i)
            path.remove(candidates[i])
            sum -= candidates[i]
        }
    }

private fun backTrack1(candidates: IntArray, target: Int, startIndex: Int, used: BooleanArray, layer: Int) {
    if (sum == target) {
        result.add(path.toList())
        println(path)
        return
    }

    for (i in startIndex until candidates.size) {
        if (sum + candidates[i] > target) { // 这样判断更好，因为是生序的数组，右边的枝没必要
            return
        }
        println("layer$layer i: $i candidates[i]: ${candidates[i]}   used: ${used[i]}")
        if (i > 0 && candidates[i] == candidates[i - 1] && !used[i - 1]) {
            println("continue ${candidates[i]}")
            continue
        }
        path.add(candidates[i])
        sum += candidates[i]
        used[i] = true
        println("path $path")
        backTrack1(candidates, target, i + 1, used, layer + 1) // 经过日志排查后, i + 1之前写的是 startIndex +1, 第二层报错
        path.remove(candidates[i])
        println("path backTrack $path")
        sum -= candidates[i]
        used[i] = false
    }
}

40.组合总和 II

https://www.bilibili.com/video/BV12V4y1V73A/

这一题的 [10,1,2,7,6,1,5]，有两个1，可能都和7组成了[1,7]就重复了，这里就是要去掉这种重复。

一开始想不到去重的思路。

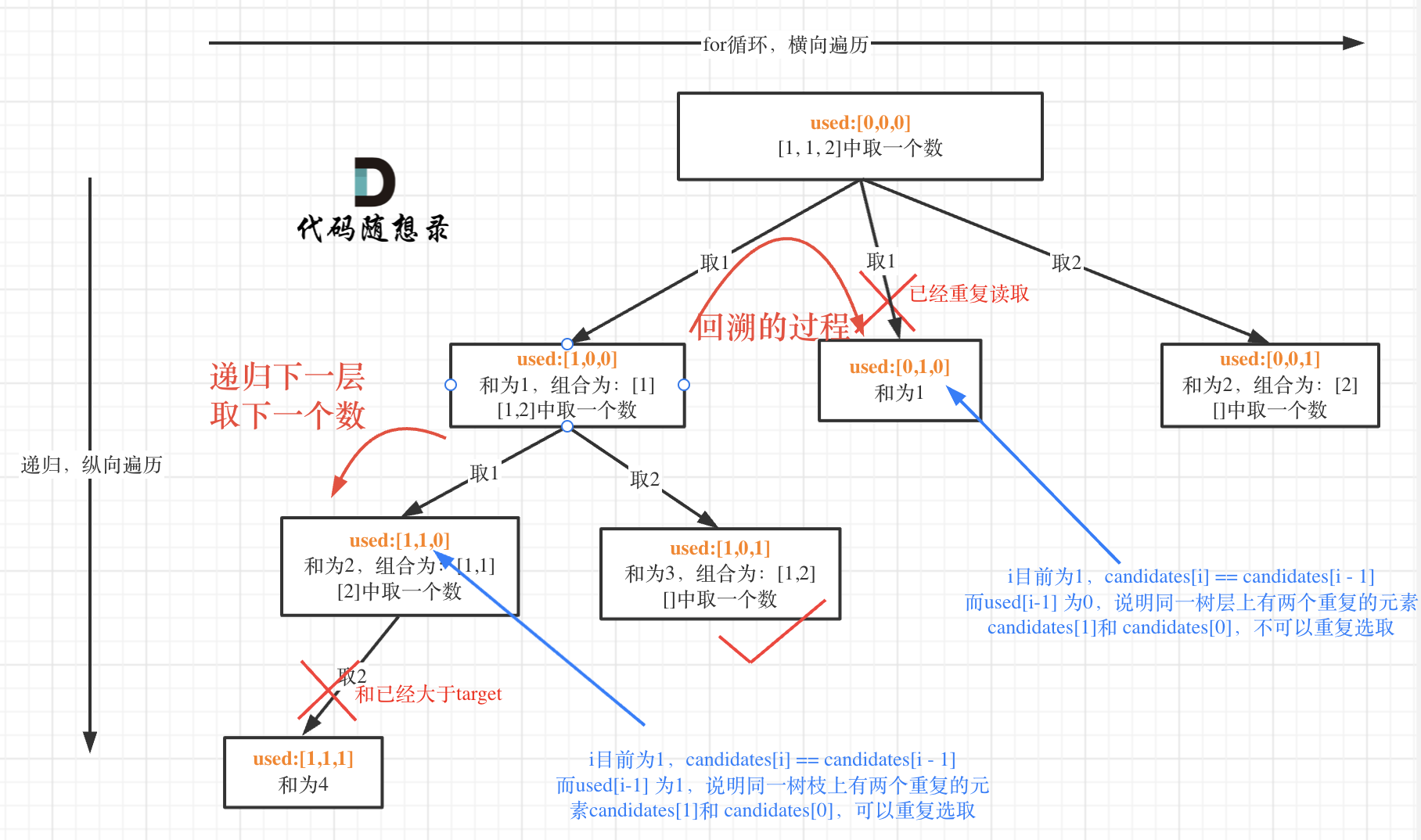
看了视频，对应这个图. 重复的原因在于树宽第二次取1的地方，因为第1次取1，已经包括了第二次取1的所有树枝。所以把第二次取1的树枝剪掉既可。
剪枝条件1：candidates[i] == candidates[i - 1]
剪枝条件2: 通过设置used数组，只有used[i - 1] 是false才有意义, used[i - 1]= false ,说明数组的第一个1没有取，取的是第二个1，结果是[1,2]，所以可以舍弃掉，否则导致和第一次的取第一个1和下一层取2,结果是[1,2]重复了。这样判断就可以把第二次取1的这个枝干给剪掉。也叫树层去重。

var sum = 0
val path = ArrayList<Int>()
val result = ArrayList<List<Int>>()

fun combinationSum2(candidates: IntArray, target: Int): List<List<Int>> {
    Arrays.sort(candidates)
    println(candidates.joinToString())
    val used = BooleanArray(candidates.size)
    backTrack(candidates, target, 0, used, 0)
    return result
}

private fun backTrack(candidates: IntArray, target: Int, startIndex: Int, used: BooleanArray, layer: Int) {
    if (sum > target) {
        return
    }
    if (sum == target) {
        result.add(path.toList())
        println(path)
        return
    }

    for (i in startIndex until candidates.size) {
        println("layer$layer i: $i candidates[i]: ${candidates[i]}   used: ${used[i]}")
        if (i > 0 && candidates[i] == candidates[i - 1] && !used[i - 1]) {
            println("continue ${candidates[i]}")
            continue
        }
        path.add(candidates[i])
        sum += candidates[i]
        used[i] = true
        println("path $path")
        backTrack(candidates, target, i + 1, used, layer + 1) // 经过日志排查后, i + 1之前写的是 startIndex +1, 第二层报错
        path.remove(candidates[i])
        println("path backTrack $path")
        sum -= candidates[i]
        used[i] = false
    }
}

131.分割回文串

1 2	输入：s = "aab" 输出：[["a","a","b"],["aa","b"]]

没想明白 [[“a”,”a”,”b”],[“aa”,”b”]] 这个数组是怎么弄出来的。

https://www.bilibili.com/video/BV1c54y1e7k6

这题是边看答案变做出来的。

131.分割回文串

根据上图可以这样理解，

DFS递归是纵向切割， a|ab 取[a], a|a|b 取 [a,a] , a|a|b| 最终到叶子节点取 [a,a,b]，到终点。
for循环是横向切割。
val str = s.substring(startIndex,i+1) // 这个也很关键，startIndex作为分割的起点

这题类似于树中符合条件的所有的路径，一旦纵向路径中，有一个不符合条件[a,ab] ab不符合，就直接回溯去其他路径.所以放if里判断递归会更好。

val result = ArrayList<List<String>>()
private val path = ArrayList<String>()
fun partition(s: String): List<List<String>> {
    backTrack(s, 0)
    return result
}

private fun backTrack(s: String, startIndex: Int) {
    if (startIndex >= s.length) { // 纵向到叶子节点，就网上回溯
        result.add(path.toList())
        return //可以用
    }
    for (i in startIndex until s.length) {  //for循环是 横向切割
        if (isPalindromeNum(s,startIndex,i+1)){ // 判断startIndex,到 i+1是否是回文串
            val str = s.substring(startIndex,i+1) // 这个也很关键，startIndex作为分割的起点
            path.add(str)
          
       // backTrack(s, i + 1)    //递归是 纵向切割，也没有循环。这个放if里面可能更好.
       // path.removeAt(path.size-1)
        }else{
            continue // 如ab不是回文串，也不用继续了 
        }
        backTrack(s, i + 1)    //递归是 纵向切割，也没有循环。这个放if里面可能更好.
        path.removeAt(path.size-1)
    }
}

fun isPalindromeNum(str: String,start:Int,end:Int): Boolean {
    if (str.isEmpty()) {
        return false
    }
    val charArray = str.substring(start,end)
    for (i in 0 until charArray.length / 2) {
        if (charArray[i] != charArray[charArray.length - 1 - i]) {
            return false
        }
    }
    return true
}

优化解法

对判断是否回文串的优化.

93.复原 IP 地址

我的分析

这题和上面131类似，可以通过切割方式解决。

ip地址都有四位，需要切割4次，所以树的深度是4。也是回溯终止条件之一，startIndex是切割线。(应该是i+1是切割线，否则只能分割一个字母)
选取有效的ip, 前导不为0，只能是数字。
<255 , 可以限制树的宽度。

我写完代码后，切割成这样 2.5.5.2，不是全部的数字，没想到什么方式能切割所有的数字。

s.substring(startIndex, s.length) 先分割前三个，然后判断最后一个字符串，这样就能分割所有的字母。

startIndex解释，下面这张图更清楚，第一层取元素2.

78.子集

93.复原IP地址

val result = ArrayList<String>()
val path = ArrayList<String>()
fun restoreIpAddresses(s: String): List<String> {
    backTrack(s, 0, 0)
    return result
}

private fun backTrack(s: String, startIndex: Int, layer: Int) {
  // 看了随想录解法，这里加上终止条件会更好。
    if (layer == 3) {   // 第三个分割线
        val substring = s.substring(startIndex, s.length) // 这里的方式就解决了，分割所有子串的问题，最后一次分割，直接到字符串的终点。
        if (isValid(substring)) {
            path.add(substring)
            result.add(path.toList().joinToString(separator = "."))
            path.removeAt(path.size-1) // 最后的字符串回溯
        }
        return
    }
    for (i in startIndex until s.length) {
        val substring = s.substring(startIndex, i + 1)
        if (isValid(substring)) {
            path.add(substring)
            backTrack(s, i + 1, layer + 1) // 注意我这里经常传错用 startIndex,如果第一次已经分割到了超过第2个位置，那么就应该传这个位置，
            path.removeAt(path.size-1)
        }
    }
}

// 判断字符串s在左闭又闭区间[start, end]所组成的数字是否合法
private fun isValid(s: String): Boolean {
    val start = 0
    val end = s.length - 1
    if (start > end) {
        return false;
    }
    if (s[start] == '0' && start != end) { // 0开头的数字不合法
        return false;
    }
    var num = 0;
    for (i in start..end) {
        if (s[i] > '9' || s[i] < '0') { // 遇到非数字字符不合法
            return false;
        }
        num = num * 10 + (s[i] - '0');
        if (num > 255) { // 如果大于255了不合法
            return false;
        }
    }
    return true;
}

78. 子集

78.子集

这题把上图画出来后，还是比较简单的。只要把所有步数情况添加就可以了。

val result = ArrayList<List<Int>>()
val path = ArrayList<Int>()
fun subsets(nums: IntArray): List<List<Int>> {
    backTrack(nums, 0)
    return result
}

private fun backTrack(nums: IntArray, startIndex: Int) {
    result.add(path.toList()) // 这棵树所有的步长，都添加
    for (i in startIndex until nums.size) {
        path.add(nums[i])
        backTrack(nums, i + 1) // 注意
        path.remove(nums[i])
    }
}

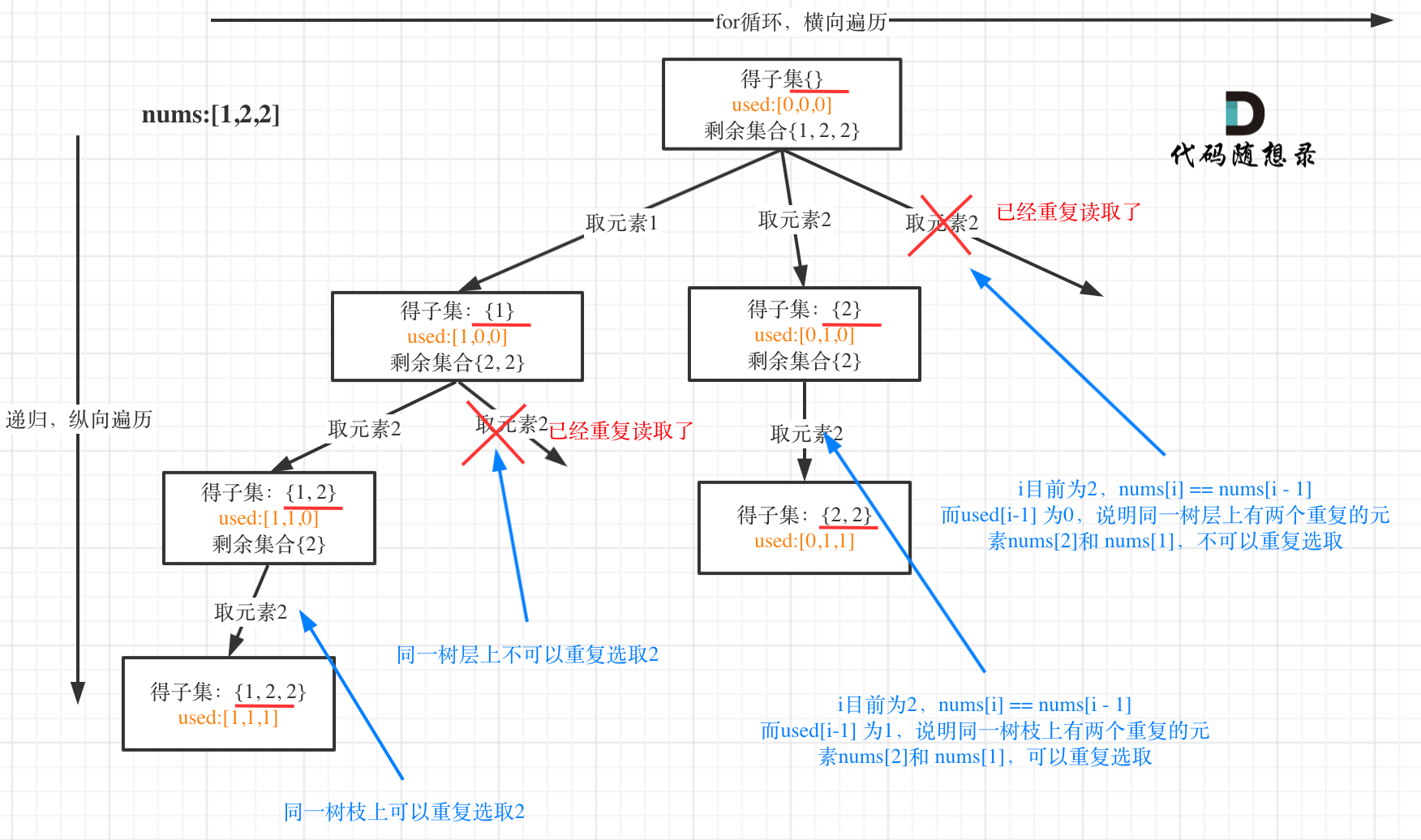
90.子集 II

90.子集II

第一层第二列取元素2的时候，此时子集就有2了，第三列再取就重复了。

从图中可以看出，同一树层上重复取2 就要过滤掉，同一树枝上就可以重复取2，因为同一树枝上元素的集合才是唯一子集！

class Solution {
    private val result = ArrayList<List<Int>>()
    private val path = ArrayList<Int>()
    fun subsetsWithDup(nums: IntArray): List<List<Int>> {
        Arrays.sort(nums)
        val used = BooleanArray(nums.size)
        backTrack(nums, used, 0)
        return result
    }

    private fun backTrack(nums: IntArray, used: BooleanArray, startIndex: Int) {
        result.add(path.toList())
        for (i in startIndex until nums.size) {
            if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {
                continue
            }
            used[i] = true
            path.add(nums[i])
            backTrack(nums,used,i+1)
            path.remove(nums[i])
            used[i] = false
        }
    }
}

!used[i - 1] 这个条件是判断树层的条件，否则会把树枝给剪掉了。

补充

本题也可以不使用used数组来去重，因为递归的时候下一个startIndex是i+1而不是0。

随想录这句没理解。

491.递增子序列

不能排序,所以子集中used解法不行
树枝中小心判断大小。

https://www.bilibili.com/video/BV1EG4y1h78v/

一开始按照下面子集的解法做的,但是存在问题，子集是经过排序后的，然后nums[i] == nums[i - 1] && !used[i - 1]这样的条件判断，这题不能排序的，所以情况不一样。

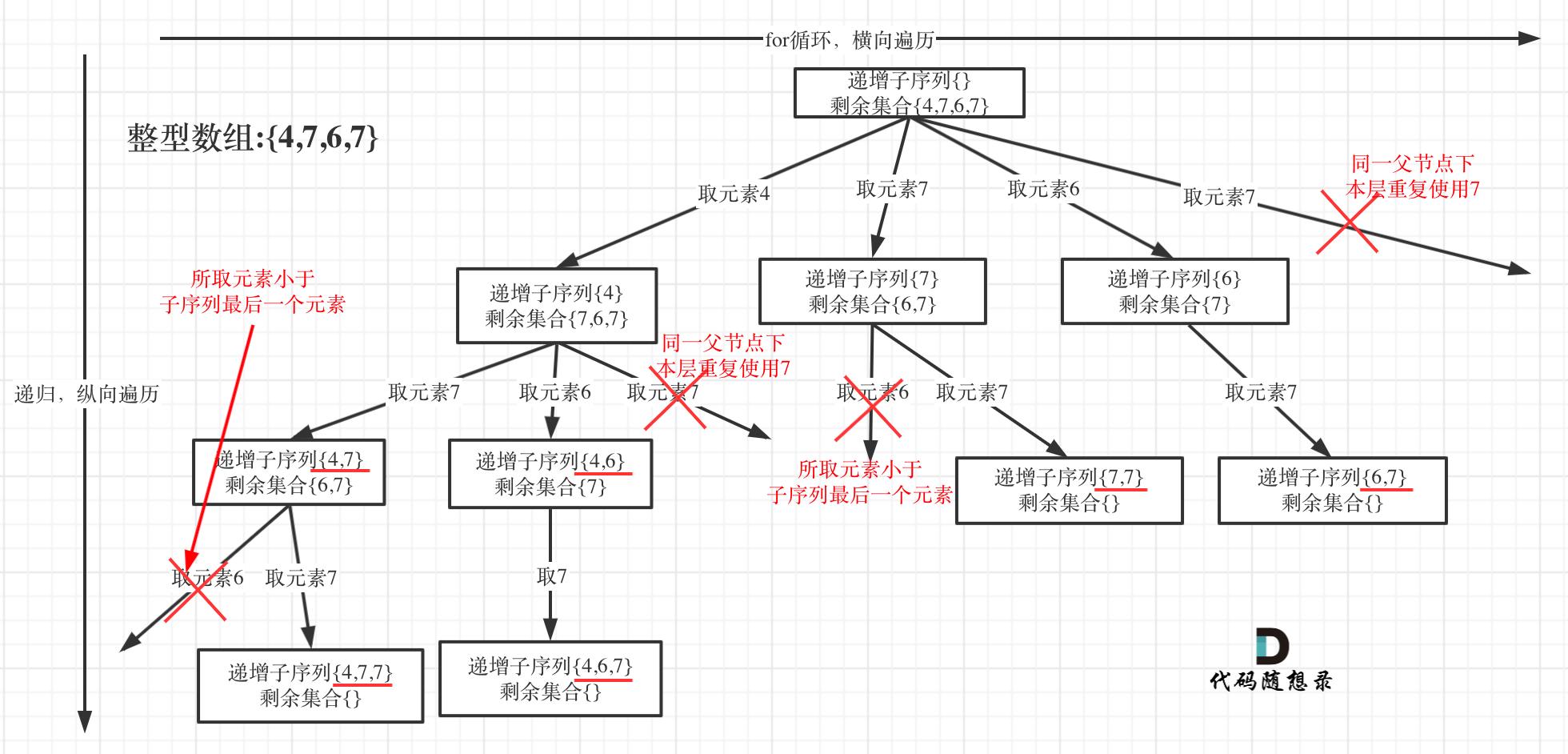
private fun backTrack(nums: IntArray, used: BooleanArray, startIndex: Int) {
    if (path.size > 1) {
        result.add(path.toList())
    }
    for (i in startIndex until nums.size) {
        if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {
            continue
        }
        if (i > 0 && nums[i] < nums[i - 1]){
            break
        }
        path.add(nums[i])
        used[i] = true
        backTrack(nums,used,i+1)
        path.remove(nums[i])
        used[i] = false
    }
}

491. 递增子序列1

上图可以看到，树层中是不能重复的，因为签名的 7包含后面7的所有情况。

    private val result = ArrayList<List<Int>>()
    private val path = ArrayList<Int>()

    fun findSubsequences(nums: IntArray): List<List<Int>> {
        backTrack(nums, 0, 0)
        return result
    }

    private fun backTrack(nums: IntArray, startIndex: Int, layer: Int) {
        if (path.size > 1) {                      //  至少有两个元素
            result.add(path.toList())
        }
        val set = mutableSetOf<Int>()             // 树层中是否包含 相同的元素。
        for (i in startIndex until nums.size) {
//            println("startIndex $startIndex set $set")
            if (layer == 0) {
                println("layer  set $set")
            }
            if ((path.isNotEmpty() && nums[i] < path.last()) || set.contains(nums[i])) { // 小于上一个元素，这个分支以下不用走了， set树层中包含相同的与元素。
                continue
            }
            set.add(nums[i])  //因为是判断树层，而且是每一层都局部会new 一个set，所以这个没有回溯。
            path.add(nums[i])
            backTrack(nums, i + 1, layer + 1)
            path.remove(nums[i])
        }
    }

private fun backTrack(nums: IntArray, startIndex: Int, layer: Int) {
    if (path.size > 1) {
        result.add(path.toList())
    }
    val used = IntArray(201) // -100 <= nums[i] <= 100 ， 包括 0
    for (i in startIndex until nums.size) {
        if ((path.isNotEmpty() && nums[i] < path.last()) || used[nums[i] + 100] == 1) {
            continue
        }
        used[nums[i] + 100] = 1
        path.add(nums[i])
        backTrack(nums, i + 1, layer + 1)
        path.remove(nums[i])
    }
}

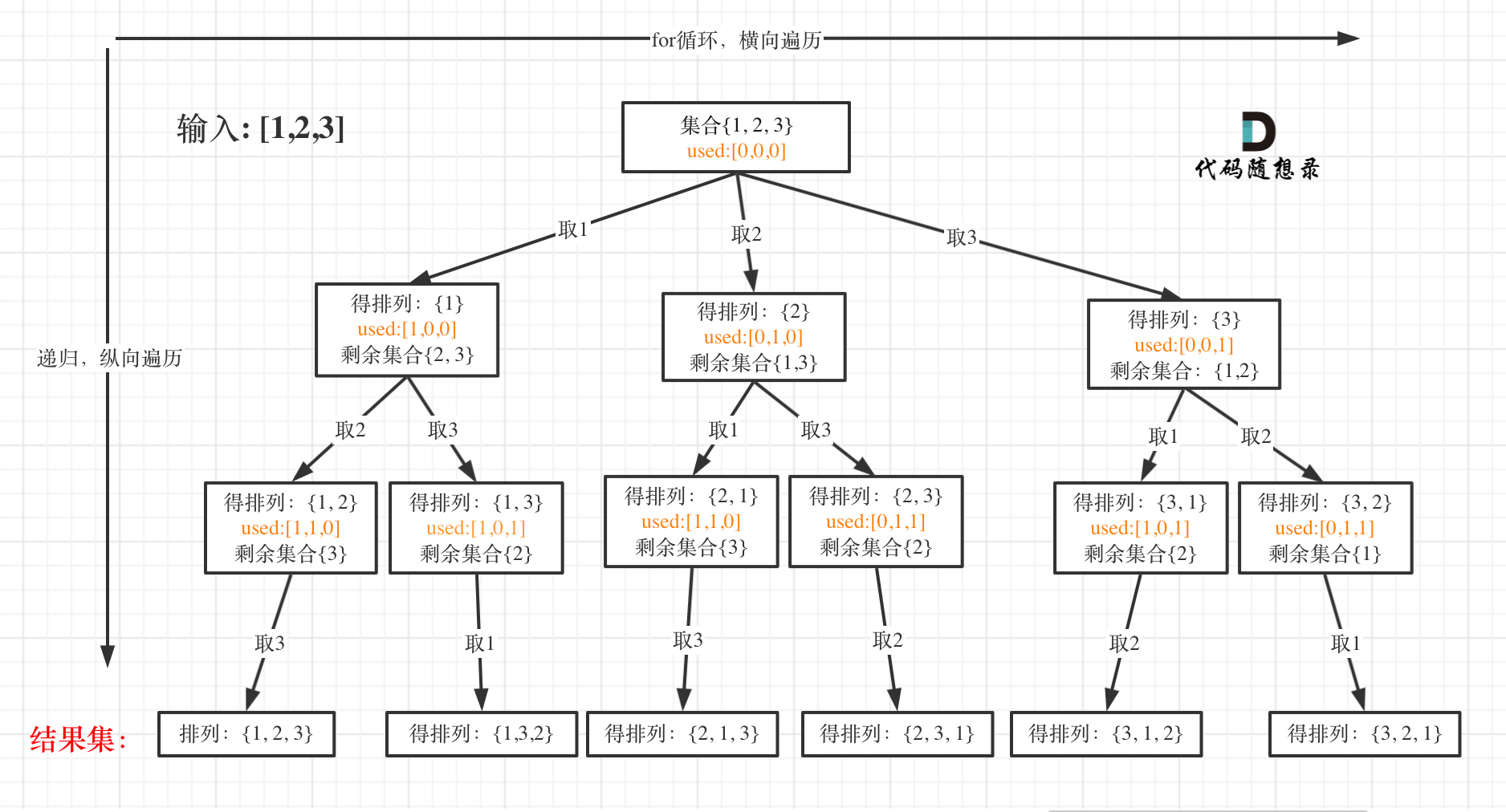
46全排列

[1,2,3] 选了2之后， 1，3 就不知道从哪里开始了，子集问题有个startIndex

我的解法

private val result = ArrayList<List<Int>>()
private val path = ArrayList<Int>()
fun permute(nums: IntArray): List<List<Int>> {
    val size = nums.size
    val used = BooleanArray(size)
    backTrack(nums, used)
    return result
}

private fun backTrack(nums: IntArray, used: BooleanArray) {
    println(path)
  //if (totalUsed(used)) {
    if (totalUsed(used)) {
        result.add(path.toList())
        return
    }
    for ((index, value) in nums.withIndex()) {
        if (used[index]) {
            continue
        }
        path.add(nums[index])
        used[index] = true
        backTrack(nums, used)
        path.remove(nums[index])
        used[index] = false
    }
}

private fun totalUsed(used: BooleanArray): Boolean {
    return used.contains(false).not()
}

先画图分析

46.全排列

单测中把数据打印出来，能大概理清这种思路，

[]
[1]
[1, 2]
[1, 2, 3]
[1, 3]
[1, 3, 2]
[2]
[2, 1]
[2, 1, 3]
[2, 3]
[2, 3, 1]
[3]
[3, 1]
[3, 1, 2]
[3, 2]
[3, 2, 1]
[[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]]

47.全排列 II

我的解法有一点点问题[2,2,1,1]这个跑步过去,path.removeAt(path.lastIndex),看了随想录的解法和我没区别，才发现这里的。

思路

和组合去重没区别 ,(index > 0 && nums[index] == nums[index - 1] && !used[index - 1])重复元素，树层去重
全排列使用过的元素。

    private val path = ArrayList<Int>()
    private val result = ArrayList<List<Int>>()
    fun permuteUnique(nums: IntArray): List<List<Int>> {
        Arrays.sort(nums)
//        nums.printIntArray()
        val used = BooleanArray(nums.size)
        backTrack(nums, used)
        return result
    }

//    private fun backTrack(nums: IntArray, used: BooleanArray) {
//        println(path)
//        if (path.size == nums.size) {
//            result.add(path.toList())
//            return
//        }
//        for ((index, value) in nums.withIndex()) {
//            if (used[index] || (index > 0 && nums[index] == nums[index - 1] && !used[index - 1])) {
//                continue
//            }
//            used[index] = true
//            path.add(value)
//            backTrack(nums, used)
//            used[index] = false
//            path.remove(value)
//        }
//    }

    private fun backTrack(nums: IntArray, used: BooleanArray) {
        println(path)
        if (path.size == nums.size) {
            result.add(path.toList())
            return
        }
        for (index in nums.indices) {
            if ((index > 0 && nums[index] == nums[index - 1] && !used[index - 1])) {
                continue
            }
            if (used[index]) {
                continue
            }
            used[index] = true
            path.add(nums[index])
            backTrack(nums, used)
            path.removeAt(path.lastIndex) // 用path.remove(value)是有问题的，会把所有的这个元素删除掉，46没问题是因为没有重复元素，leetcode removeLast() cannot build
            used[index] = false
        }
    }

332.重新安排行程

随想录解法那个数组处理没看明白

这里用到的回溯，就是目的地可能有多个。

https://leetcode.cn/problems/reconstruct-itinerary/solutions/654811/java-bu-yong-ou-la-zhi-yong-hui-su-si-lu-4v83/

看了他的视频

给定的tickets转成 from to 的结构,就可以知道出发点对应的，到达点和到达点的线路数。 // 这个数据处理也是有点麻烦的。
根据多个到达点回溯，找到最合适的路径
如果到达点的是线路是0，那么找下一题跳线路。
遇到的机场个数path ==航班数量+

putIfAbsent

https://blog.csdn.net/hbtj_1216/article/details/75093428

val path = ArrayList<String>()
fun findItinerary(tickets: List<List<String>>): List<String> {
    //1. list转成 from to 的结构
    //2. 回溯找到最合适的路径
    //3.  遇到的机场个数path ==航班数量+
    val hashMap = HashMap<String, TreeMap<String, Int>>()
    tickets.stream().forEach { ticket ->
        val from = ticket[0] // 出发地
        val to = ticket[1]  //目的地

        hashMap.putIfAbsent(from, TreeMap())
        val treeMap = hashMap[from] ?: TreeMap()  //获取出发地对应的容器TreeMap,如果之前没用过的出发地key,那么新建一个容器TreeMap
        treeMap[to] = treeMap.getOrDefault(to, 0) + 1 // 容器内，目的地的个数++,一开始这里写的有问题。
    }
    path.add("JFK") // 所有这些机票都属于一个从 JFK（肯尼迪国际机场）出发的先生，所以该行程必须从 JFK 开始。
    backTrack(hashMap, tickets.size)
    return path
}

private fun backTrack(hashMap: HashMap<String, TreeMap<String, Int>>, ticketSize: Int): Boolean {
    if (path.size == ticketSize + 1) {
        return true
    }
    // 1.根据path找到出发点,从hashmap根据出发点找到对应的 可能多个到达点
    // 2. 多个可能的目的地进行回溯.
    val recentTo = path[path.size - 1] //path.last() LeetCode build failed
    val toDestinations = hashMap[recentTo]
    if (toDestinations.isNullOrEmpty()) return false
    for (to in toDestinations) {// forEach也行, for习惯点
        if (to.value == 0) {
            continue
        }
        path.add(to.key)
        to.setValue(to.value - 1)
        if (backTrack(hashMap, ticketSize)) {
            return true
        }
        path.removeAt(path.size - 1)
        to.setValue(to.value + 1)
    }
    return false
}

51.N 皇后

这题思路不难，实现还是有难度，主要是皇后冲突代码不好理解，https://www.bilibili.com/video/BV1bK4y1n7iq

大概11分钟，判断皇后位置的冲突情况。

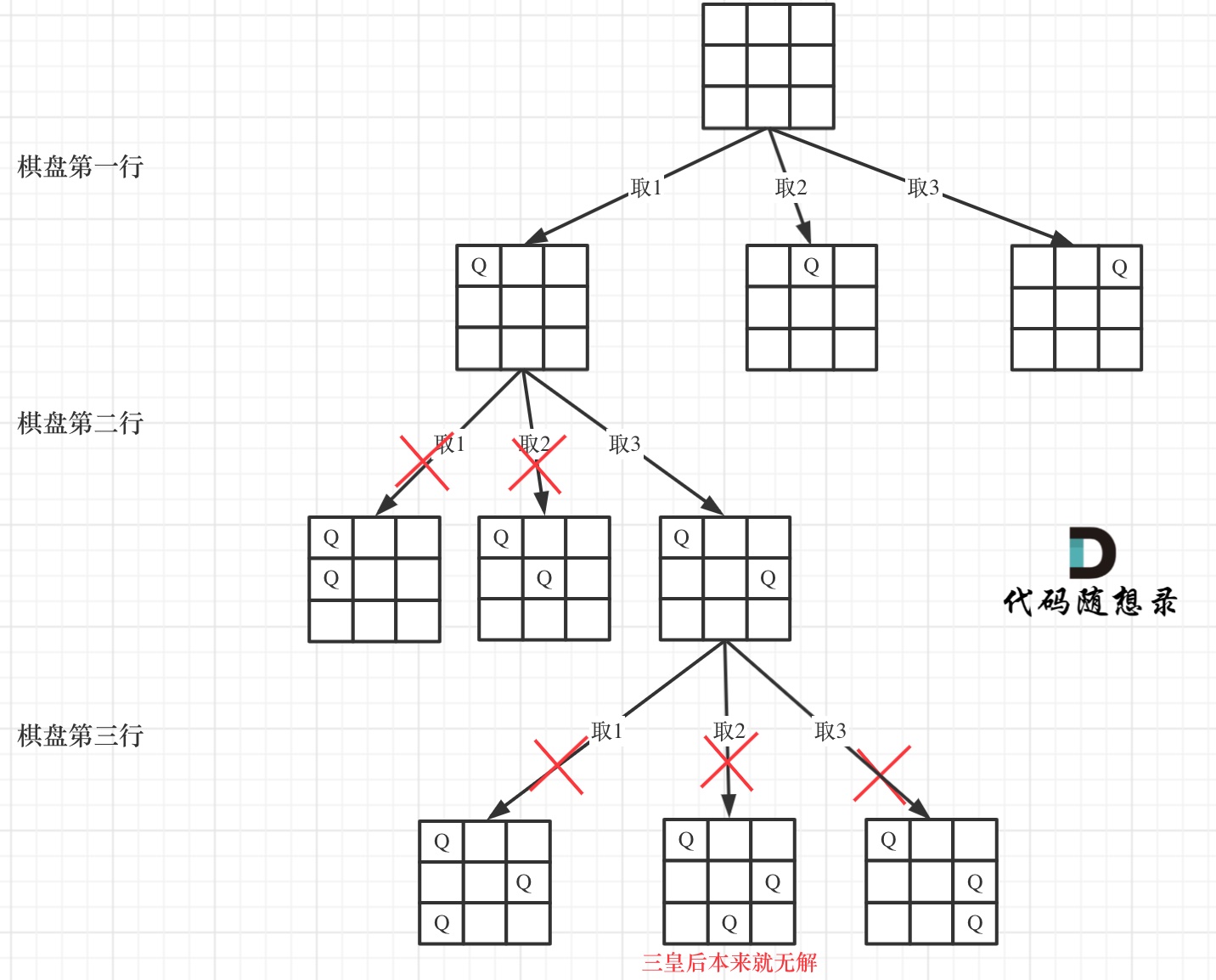
这一题思路就是主要首先行，然后列摆放皇后问题，然后回溯。
还一个就是将要放下皇后的位置之前，8个方向只用考虑3个,确定左上，正上方，右上方的皇后是否存在。当前行不用考了，因为每行一个，后面的更不看了，因为还没放皇后.
最后就是要注意边界的问题，二刷的时候尤其注意这个。

List<List<String>> result = new ArrayList<>();

public List<List<String>> solveNQueens(int n) {
    //1. 初始化棋盘放上.
    char[][] chessBoard = new char[n][n];
    for (char[] c : chessBoard) {
        Arrays.fill(c, '.');
    }
    // 2. 开始放Queue,首先从行开始，一行一行回溯的放， 然后每一行开始从第1列开始。
    // 3. 每次新的一行开始放Queue时，要考虑当前位置列的 前面的列有没有Queue,
    // 当前位置的左边45度和135度有没有Queue,对于当前行和后面的行和斜对角不用考虑，因为每一行只有一个Queue,后面的行更是没有。
    //4 。只有能放下，才会放后续的，然后进行回溯.
    //5. 当放下的Queue时最后一行n时，递归结束，开始收集结果。
    backTrack(n, 0, chessBoard);
    return result;
}

private void backTrack(int n, int row, char[][] chessBoard) {
    if (n == row) {
        result.add(Array2List(chessBoard));
        return;
    }
    for (int column = 0; column < n; ++column) {
        if (isValid(row, column, chessBoard, n)) { // row,column待放入Queue的位置
            chessBoard[row][column] = 'Q';
            backTrack(n, row + 1, chessBoard);
            chessBoard[row][column] = '.';
        }
    }
}

private boolean isValid(int pRow, int pColumn, char[][] chessBoard, int n) {
    for (int i = 0; i < pRow; ++i) { //列
        if (chessBoard[i][pColumn] == 'Q') {
            return false;
        }
    }
    for (int x = pRow - 1, y = pColumn - 1; x >= 0 && y >= 0; x--, y--) { //左上角 首次==边界错了
        if (chessBoard[x][y] == 'Q') {
            return false;
        }
    }
    for (int x = pRow - 1, y = pColumn + 1; x >= 0 && y <= n - 1; x--, y++) {//右上角  首次==,n-1边界错了 ,y < n - 1一开始写成这样，找了半天
        if (chessBoard[x][y] == 'Q') {
            return false;
        }
    }
    return true;
}

public List Array2List(char[][] chessboard) {
    List<String> list = new ArrayList<>();

    for (char[] c : chessboard) {
        list.add(String.copyValueOf(c));
    }
    return list;
}

这题for里面有x,y两个变量，kotlin不好弄，就用java了。

37.解数独

随想录讲解.

https://www.bilibili.com/video/BV1TW4y1471V/

20230102104449

https://xiaochen1024.com/video?id=6285f1b6ede03c002e46b218

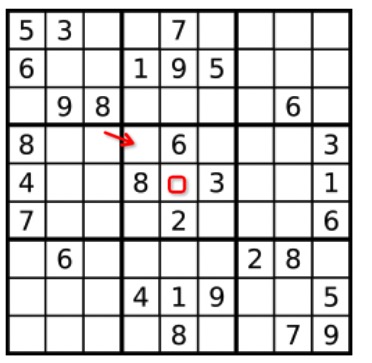
根据下面公式可以找到 3 *3的开始位置。

val startRow = (row / 3) * 3    
val startColumn = (column / 3) * 3

把红方框代入进去， val 3 = (4 / 3) * 3 就是红色箭头的位置。

// 1.先行 后列的顺序，找到字符位 '.'的空格，填入 1 - 9 的数字
// 2.填入后，开始回溯
// 3.填入空格的时候，如果没有返回true,if就返回false
// 4. 如果全部填满了都没返回true,此时说明已经到了叶子节点，直接返回true.
fun solveSudoku(board: Array<CharArray>): Unit {
    backTrack(board)
}

private fun backTrack(board: Array<CharArray>): Boolean {
    for (i in board.indices) {   // 遍历行
        for (j in board[0].indices) {// 遍历列
            if (board[i][j] == '.') {
                for (k in '1'..'9') {
                    if (isValid(i, j, k, board)) {
                        board[i][j] = k
                        if (backTrack(board)) {
                            return true
                        }
                        board[i][j] = '.'
                    }
                }
                return false //放上面一层，循环后直接返回false了,// 9个数都试完了，都不行，那么就返回false
            }
        }
    }
    return true
}

private fun isValid(row: Int, column: Int, k: Char, board: Array<CharArray>): Boolean {
    for (i in board[0].indices) { // 判断行里是否重复,一开始不理解很多解法包括，随想录用的是9,这样如果不是9*9就有问题了,原来题目给的就是9*9的方格
        if (board[row][i] == k) {
            return false
        }
    }
    for (i in board.indices) {  // 判断列里是否重复
        if (board[i][column] == k) {
            return false
        }
    }
    val startRow = (row / 3) * 3    
    val startColumn = (column / 3) * 3
    for (i in startRow until (startRow + 3)) {  // 判断9方格里是否重复
        for (j in startColumn until startColumn + 3) {
            if (board[i][j] == k) {
                return false
            }
        }
    }
    return true
}

DataStructure

#LEETCODE

LC-backtrack-combination

https://noteforme.github.io/2022/10/30/LC-backtrack-combination/

Author

Jon

Posted on

October 30, 2022

Licensed under

viewBinding Previous

AppLink Next