LC-DP

Labuladong

https://www.bilibili.com/video/BV1XV411Y7oE

  1. 重叠子问题
  2. 状态转移方程 (最关键)
  3. 最优子结构
  1. 明确状态
  2. 明确 选择
  3. 明确dp函数/数组的定义
  4. 明确base case

随想录

https://www.bilibili.com/video/BV13Q4y197Wg

动规5部曲

对于动态规划问题，我将拆解为如下五步曲，这五步都搞清楚了，才能说把动态规划真的掌握了！

1
2
3
4
5
1. 确定dp数组（dp table）以及下标的含义
2. 确定递推公式
3. dp数组如何初始化
4. 确定遍历顺序
5. 举例推导dp数组

动态规划解法代码框架

20230701162055

509. 斐波那契数

随想录 迭代递推

自底向上

通过for循环递推出 dp[n]的值，一开始解的时候写成了 dp[n] = dp[n - 1] + dp[n- 2] 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
    /**
     * 随想录视频思路解法1
     */
    fun fib1(n: Int): Int {
//        println(n)
        if (n == 0) return 0
        else if (n == 1) return 1
        val dp = IntArray(n+1)
        dp[0] = 0
        dp[1] = 1
        for (i in 2..n) {
            dp[i] = dp[i - 1] + dp[i - 2]
//            println(" dp[n - 1]= ${ dp[n - 1]}  dp[n - 2]= ${dp[n - 2]}")
        }
        return dp[n]
    }
随想录 视频思路解法2

这种解法，dp数组空间复杂度减少了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
/**
 * 随想录视频思路解法2
 */
fun fib(n: Int): Int {
    if (n == 0) return 0
    else if (n == 1) return 1
    val dp = IntArray(2)
    dp[0] = 0
    dp[1] = 1
    var sum = 0
    for (i in 2..n) {
        sum = dp[0] + dp[1]
        println("sum $sum  dp[0]= ${dp[0]} , dp[1]= ${dp[1]}")
        dp[0] = dp[1]
        dp[1] = sum
    }
    return sum
}
labuladong

把所有计算的值先保存起来，后面需要的话先直接返回，避免重复计算.

为什么申请 n+1 数组大小

因为索引从0开始 ，后面要取memory[n]，所有就申请 n+1 大小.

自顶向下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
fun fib(n: Int): Int {
    val memory = IntArray(n + 1)
    if (memory[n] != 0) {
        return memory[n]
    } else if (n == 0) return 0
    else if (n == 1) return 1

    memory[n] = fib(n - 1) + fib(n - 2)
    return memory[n]
}


fun fib(n: Int): Int {
    if (n == 0) return 0
    if (n == 1) return 1
    return fib(n - 1) + fib(n - 2)
}

还有一种lablado解法一开始没想出来,双指针应该怎么操作

这个思路和随想录的思路2是一样的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
fun fib(n: Int): Int {
    var pre1 = 0
    var pre2 = 1
    var sum = 0

    if (n == 0) return 0
    else if (n == 1) return 1
    for (i in 2..n) {
        sum = pre1 + pre2  // 得到当前n的num
        pre1 = pre2     //移动指针
        pre2 = sum
    }
    return sum
}

70 爬楼梯

根据阶梯

0阶 1 // 需要返回1，2 = 1 +1,否则2就不正确了,正常理解应该返回0,不过递归解法，需要返回1

1阶 1

2阶 1+1 , 2 2

3阶 1+1+1, 1+2, 2+1 3

四阶 5

根据上面的推导，这个问题也类似于 斐波那契数 ， 看了随想录的视频，这个推导过程还是没看明白

看了这个视频推导明白了

https://www.bilibili.com/video/BV1G54y1X72H/ 进度条5分钟.

到达 k 只有 两种方式 , k-2过去和k-1过去，所以到k的所有情况就是 (k-2) + (k-1) ,我们这里讨论的是多少种不同的方法，而不用管k-2,k-1多少步到达k.
k
k-1
k-2
递归解法

超时

1
2
3
4
5
6
7
8
9
10
11
/**
 * 递归解法 ， 会超时
 */
fun climbStairs(n: Int): Int {
    if (n == 0) return 1 // 需要返回1，2 = 1 +1,否则2就不正确了
    if (n == 1) return 1
    val dp = IntArray(n + 1)
    dp[0] = 1
    dp[1] = 1
    return climbStairs(n - 1) + climbStairs(n - 2)
}
迭代解法
1
2
3
4
5
6
7
8
9
10
11
fun climbStairs1(n: Int): Int {
    if (n == 0) return 1
    if (n == 1) return 1
    val dp = IntArray(n + 1)
    dp[0] = 1
    dp[1] = 1
    for (i in 2..n) {
        dp[i] = dp[i - 1] + dp[i - 2]
    }
    return dp[n]
}

746 使用最小花费爬楼梯

如果要走到dp[i] 的位置， 有两种选择，dp[i-1] + cost[i-1] ，dp[i-2] + cost[i-2]， cost就是从当前位置跳出消耗的能量值，dp[i-1] 已经包含dp[0]开始的所有 消费值。 

1
dp[i] = min(dp[i-1] + cost[i-1], dp[i-2] + cost[i-2])

可以用这个推导

023-07-09-20-24-53

官方题解

这种方式比较好理解

1
2
3
4
5
6
7
8
9
fun minCostClimbingStairs(cost: IntArray): Int {
    val dp = IntArray(cost.size + 1) //要走完数组最后一步的下一步
    dp[0] = 0
    dp[1] = 0
    for (i in 2..cost.size) {
        dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2])
    }
    return dp[cost.size]
}

其他的后面在看吧

62. 不同路径

这题二叉树解法没看懂，给忘了。

递归公式的推导，

1
那么很自然，dp[i][j] = dp[i - 1][j] + dp[i][j - 1]，因为dp[i][j]只有这两个方向过来。
  1. dp数组的初始化
1
如何初始化呢，首先dp[i][0]一定都是1，因为从(0, 0)的位置到(i, 0)的路径只有一条，因为只能向右向下走，那么dp[0][j]也同理。

所以初始化代码为：

1
2
for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;

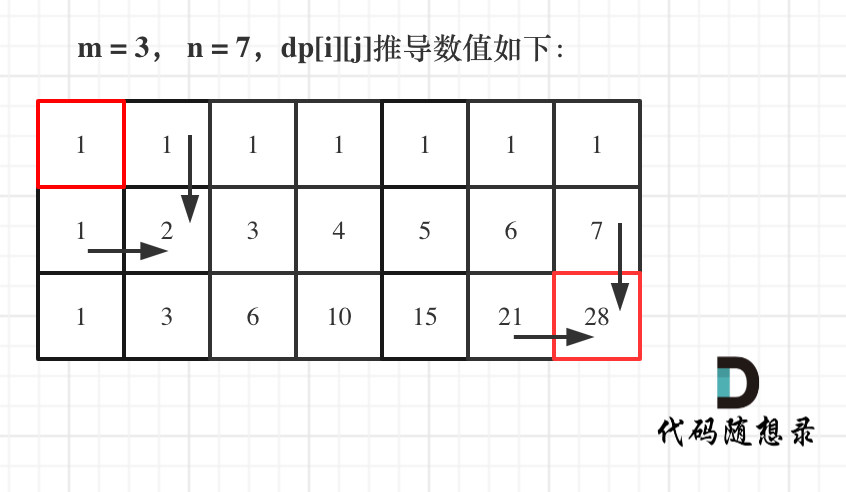
62.不同路径1

可以根据上图来推导出 dp[i][j]

i =1 时 , j 代入进去进行推导。

j = 1 : dp[i][j] = dp[i-1][j] + dp[i][j-1]

j = 2 : dp[i][j] = dp[i-1][j] + dp[i][j-1]

j = 3 : dp[i][j] = dp[i-1][j] + dp[i][j-1]

然后逐步就能推导出所有的值,注意dp[m][n] 要-1,否则会越界。

1
2
3
4
5
6
7
8
9
10
11
fun uniquePaths(m: Int, n: Int): Int {
    val dp = Array(m) { IntArray(n) }
    for (i in 0 until m) dp[i][0] = 1
    for (j in 0 until n) dp[0][j] = 1
    for (i in 1 until m) {
        for (j in 1 until n) {
            dp[i][j] = dp[i-1][j] + dp[i][j-1]
        }
    }
    return dp[m-1][n-1]
}

63. 不同路径 II

原理还是一样，从左到右,array[i][0] : array[0][0],array[1][0],array[2][0] ，从上到下 进行推导。

这一题是上一题的拓展版本

通过62题可以看到 m 是竖线，n是横线。

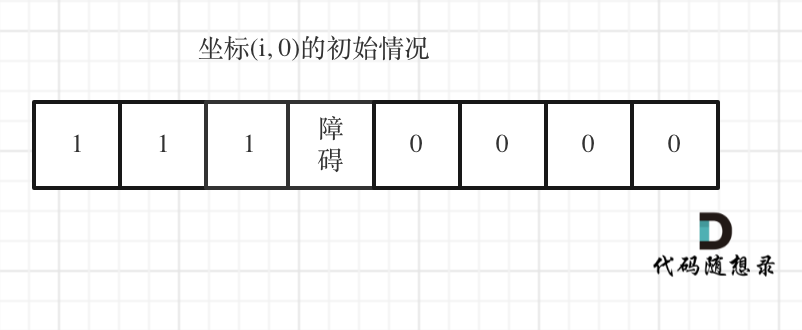
63.不同路径II

  1. [0][0] [m-1][n-1] 那么不可能有有路径往后走了。

  2. 有一点不同的是，如果是有障碍，后面就不用初始化了。

    img

  3. 还有一点不同的是，如果要找的位置没有障碍物，才有求出递推值的意义。

  1. 递推公式和前面差不多 ，在处理递推公式的时候，看上图，前一步有障碍物的时候，影响的是 dp[i-1] dp[j-1] 前一步的一个值。
  2. 后续递推的时候，碰到obstacles后，obstacles的点就是0，所以下一个点就是障碍物 0 和另一个点相加。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
fun uniquePathsWithObstacles(obstacleGrid: Array<IntArray>): Int {
    val m = obstacleGrid.size // 表示有多少个数组
    val n = obstacleGrid[0].size // 其中一个数组的长度

    if (obstacleGrid[0][0] == 1 || obstacleGrid[m-1][n-1] == 1) return 0 // if there are obstacle in these two points, will no path.

    val dp = Array(m) { IntArray(n) }
    for (i in 0 until m) { // 里面再加个条件不好加
        if (obstacleGrid[i][0] == 1) break      // when init dats, hit path , following init will 0
        dp[i][0] = 1 // 前面[i][0] i表述多少个数组
    }
    for (j in 0 until n) {
        if (obstacleGrid[0][j] == 1) break
        dp[0][j] = 1 // [0][j] 后面表述一个数组的长度
    }
    for (i in 1 until m) {
        for (j in 1 until n) {
            if (obstacleGrid[i][j] != 1) {
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
            }
        }
    }
    return dp[m - 1][n - 1]
}

343. 整数拆分

我们按照动规 5 部曲来分析先

  1. 确定dp数组（dp table）以及下标的含义

    拆分i，最大乘积是dp[i]

  2. 确定递推公式

    这一步是比较难的， 对 i 进行拆分，看了随想录的视频，有3种可能

    第一种: 拆成2个数的情况 i * j 也就是 dp[i] = i * (i-j)

    第二种：拆成2个数以上的情况 : dp[i] = i * dp[i-j]

    这种可以用6来测试拆分

    1 * 5

    2 * 4

    3 * 3

    4 * 2

    5 * 1

    上面我们可以只拆分j, 我们有必要拆分i吗，其实是没必要的， 我的理解是2 * 4 中， 2已经被 1 * 5 中的5包含了，

    那么5 拆成 2 *1 * 1 * 1 就包括了 2的情况，不知道我的理解对不对。

    第三种 : 就是 i本身。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
        fun integerBreak(n: Int): Int {
            if (n == 2) return 1  // 1+1
            val dp = IntArray(n + 1)
            dp[0] = 0
            dp[1] = 0
            dp[2] = 1
            for (i in 3..n) {
                for (j in 1 until i) {
    //                println("i $i    j $j ")
                    val a = j * (i - j)
                    val b = j * dp[i - j]
    //                maxNum = max(a, b, i)
                    println("j * (i - j)  $j * ($i - $j)  a =$a  dp[i - j] ${dp[i - j]}  b= $b ")
    //                maxNum = max(a, b,dp[i])
    //                maxNum= max(a,b)
    //                val abMax = max(a, b)
    //                println("abMax $abMax dp[$i] ${dp[i]} ")
                    dp[i] = max(a, b, dp[i]) // dp[i] 初始值是0，所以得出的值还是从a,b中拿到最大值
                }
    //            println("dp[$i]     ${dp[i]}")
            }
            return dp[n]
        }


    fun max(a: Int, b: Int, c: Int): Int {
        var max = a
        if (b > max) {
            max = b
        }
        if (c > max) {
            max = c
        }
        return max
    }

96. 不同的二叉搜索树

​

上面是i==3的情况，

root node =1的时候， left tree 0 , right tree 2种情况 , 右子树和 root node =2的树的结构是一样的。

root node =2的时候， left tree 1 , right tree 1种情况, 左，右子树和 root node =1的树的结构是一样的。

root node =3的时候， left tree 2 , right tree 0种情况. 左子树和 root node =2的树的结构是一样的。

所以 dp[3] = (root node ==1 +dp[2]) + (root node ==2 +dp[1]) + (root node ==3 +dp[2])

dp[3]，就是 元素1为头结点搜索树的数量 + 元素2为头结点搜索树的数量 + 元素3为头结点搜索树的数量

元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量

元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 * 左子树有1个元素的搜索树数量

元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 * 左子树有2个元素的搜索树数量

有2个元素的搜索树数量就是dp[2]。

有1个元素的搜索树数量就是dp[1]。

有0个元素的搜索树数量就是dp[0]。

所以dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2]

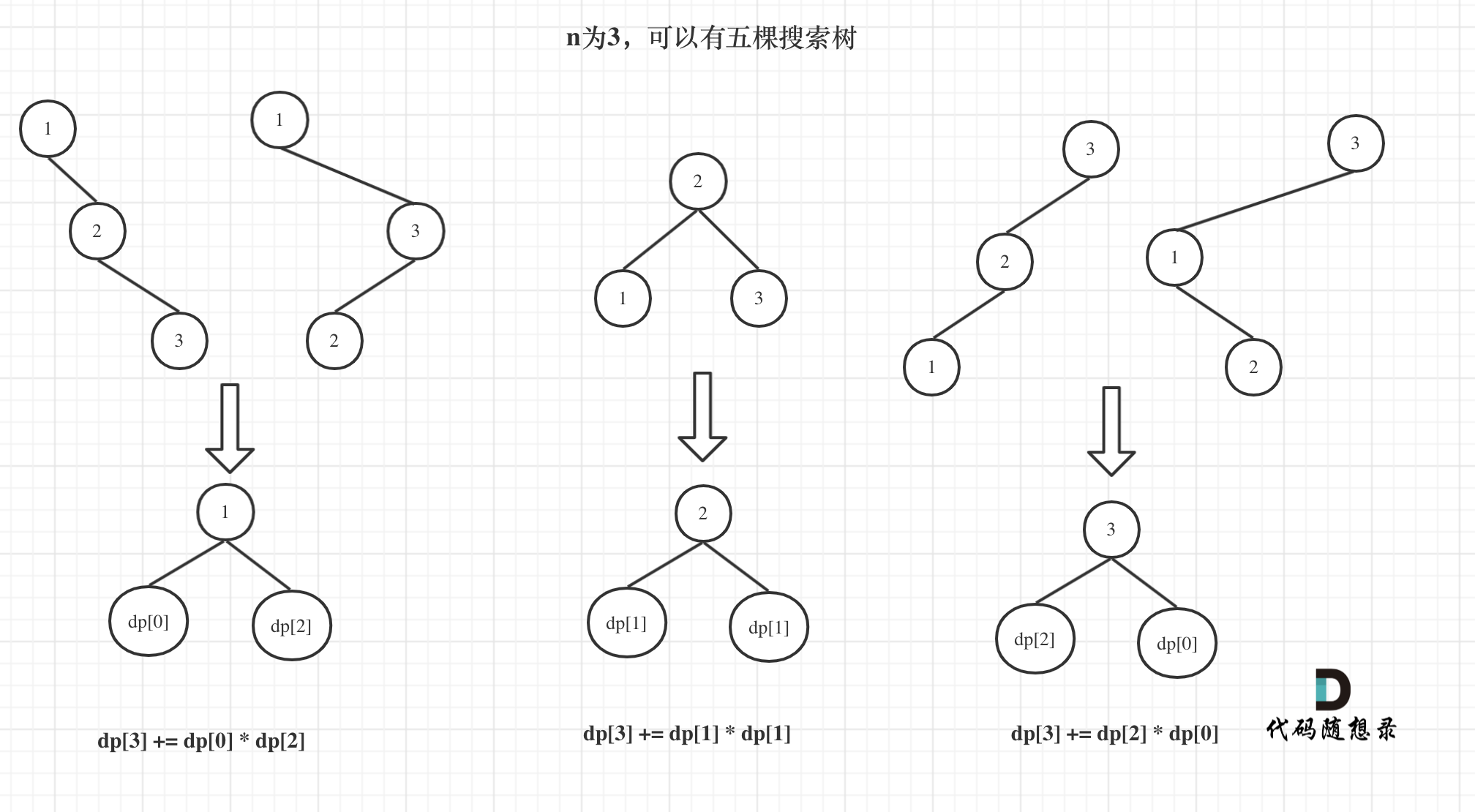
96.不同的二叉搜索树2

这个图更直观

  1. 确定dp数组（dp table）以及下标的含义目前可以根据下面推导来，确认dp数组的含义。dp[1] =1dp[2]= 2dp[3] =5
  2. 确定递推公式这个没推导出来，i j没搞清楚。把随想录的拿过来
    1
    2
    3
    4
    5
    在上面的分析中，其实已经看出其递推关系， dp[i] += dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量]

    j相当于是头结点的元素，从1遍历到i为止。

    所以递推公式：dp[i] += dp[j - 1] * dp[i - j]; ，j-1 为j为头结点左子树节点数量，i-j 为以j为头结点右子树节点数量
  3. dp数组如何初始化
  4. 确定遍历顺序
  5. 举例推导dp数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
    fun numTrees(n: Int): Int {
        // 1. 确定dp数组（dp table）以及下标的含义
        val dp = IntArray(n + 1)
        dp[0] = 1
        dp[1] = 1
        //3. dp数组如何初始化

        //4.确定遍历顺序
        for (i in 2 ..n) {
            for (j in 1 ..i) { // 注意这里边界，一开始都 没加==
//                println(" dp[$i] ${dp[i]} += (dp[j - 1] ${dp[j - 1]}  * dp[i - j]) ${dp[i - j]}  j = $j")
                dp[i] += (dp[j - 1] * dp[i - j]) //2.确定递推公式
            }
        }
        return dp[n]
    }
DataStructure
#LEETCODE
LC-DP
https://noteforme.github.io/2023/04/02/LC-DP/
Author
Jon
Posted on
April 2, 2023
Licensed under