LC_DP_BAG

Screenshot 2023-09-23 at 22.11.27.png

对于01背包，物品i，我觉得也是从0开始更好。

纯01背包:装满这个背包的最大价值。

分割等和子集：能否装满。

本题: 给一个背包容量，有多少种方式装满。

解法一

随想录

背包问题理论基础

这个视频讲的很好

https://www.bilibili.com/video/BV1jT4y1o71J/

0/1 Knapsack problem | Dynamic Programming - YouTube

https://www.bilibili.com/video/BV1cg411g7Y6/

The 0/1 Knapsack Problem (Demystifying Dynamic Programming) - YouTube

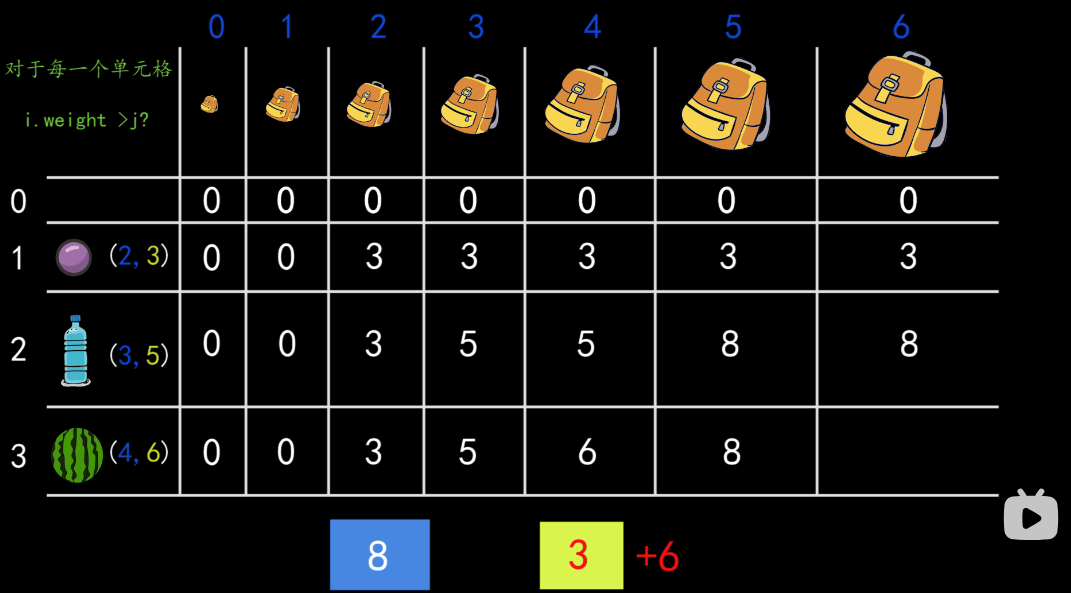
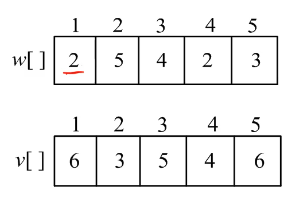
有N件物品和一个最多能背重量为W 的背包。第i件物品的重量是weight[i]，得到的价值是 value[i] 。

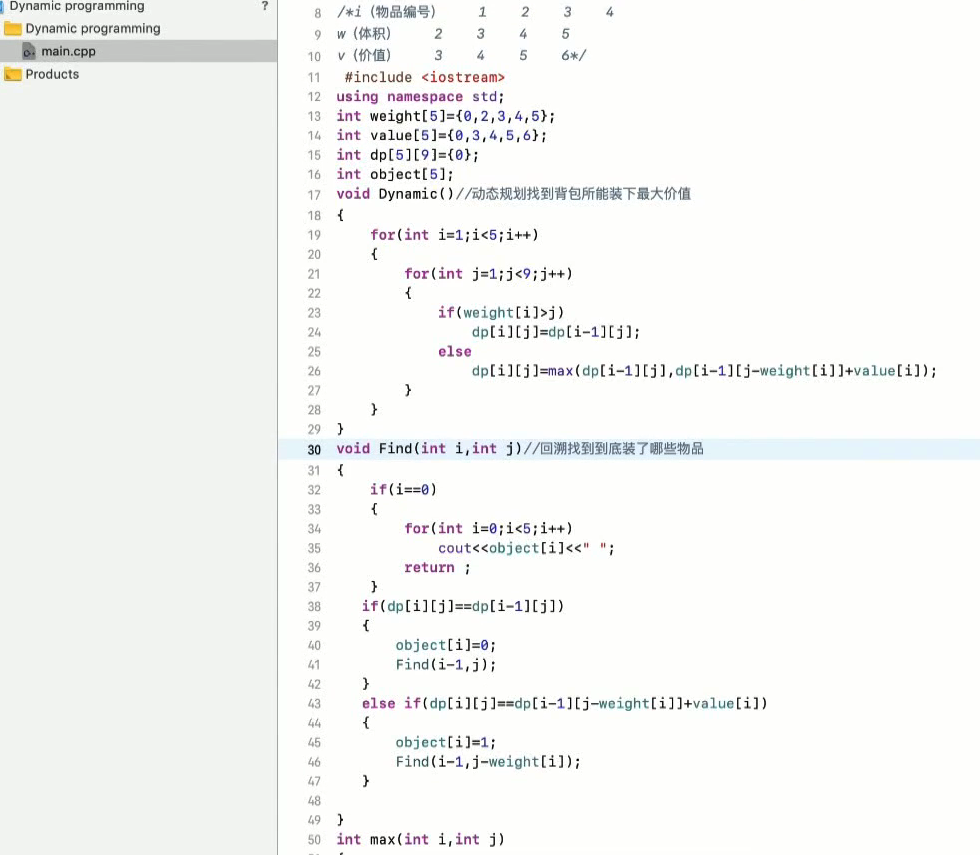
dp[i][j] 
[0,i]物品任取放容量为j的背包

不放物品i : dp[i-1][j]
放物品i :  dp[i-1][j-weight[i]] + value[i]， 那么就是前i-1种物品的选择，减去当前i物品的重量 + 当前i物品的价值，其实就转化为 i-1种物品 j-weight[i]的容量下的最大值。

dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight[i]] + value[i])

从上面的递推公式可以看出，当前值都是由左上角的值，其实我觉得是正上角，来递推出来的。dp[i-1][j]

2023-09-10-15-34

随想录的解法，物品0是第一个物品，所以X方向初始化是有值的

下面两个视频，x,y都初始化0，感觉更好。

01背包问题，这个视频讲的很好

https://www.bilibili.com/video/BV1pY4y1J7na

https://www.bilibili.com/video/BV1K4411X766

对第0行，第0行没有任何物品，在任何背包容量下，前0个物品，能装进背包的最大价值为0.

对第0列，第0列没有任何容量，在任何物品都无法放进背包，因此价值也都为0.

最后一个单元格的数字，就是我们要得到的最终答案。

j 2023-09-09-21.54.02.png

sts/LC-DP/2023-09-09-21.54.02.png)

[2,1] 放葡萄情况下：葡萄占用2，并且葡萄无法再次被选择，此时问题从背包容量为2的情况下，对前一种物品取舍选择后获得的容量，变成了背包容量最大为0的情况下，对前0种物品进行取舍选择后获得的最大价值。

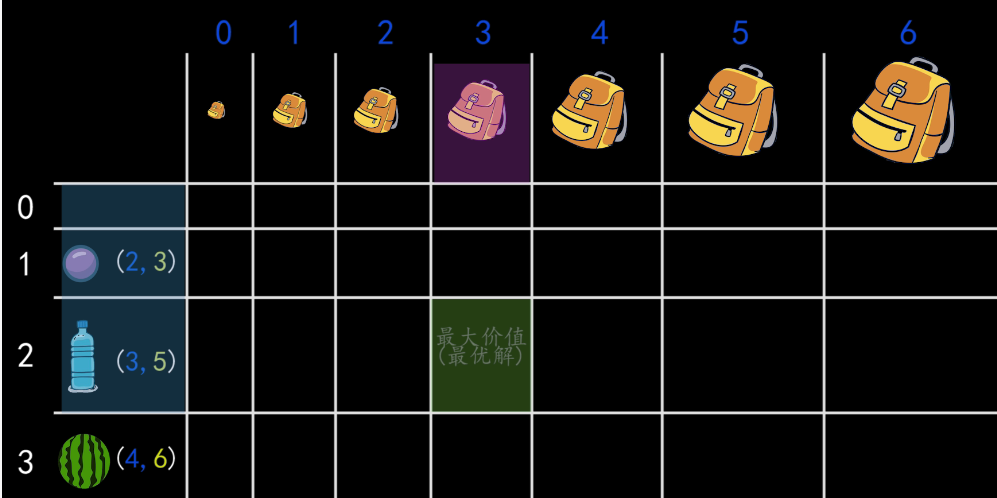
2023-09-09-21.56.02.png

第2行3列的单元格，背包容量最大为3的情况下，对前面2种物品进行选择。

对于i行j列的单元格，背包容量最大为j的情况下，对前面i种物品进行选择，能使得背包价值最大，也就是说每个单元格都是当前条件下的最优解。

下面这个代码，把x,y 0的点都初始化为0.

放入的物品

Screenshot 2023-09-24 at 16.25.54.png

Screenshot 2023-09-24 at 15.56.52.png

https://www.bilibili.com/video/BV1jT4y1o71J/

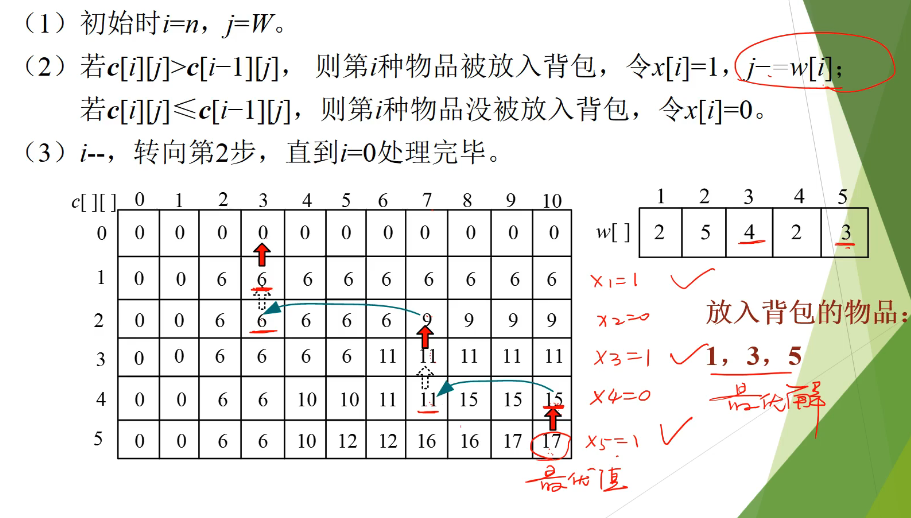
caculate what goods were added in bag. 33:00

先从dp[5][10] ,17开始，15 !=17 所以物品5放入了背包, 这个是 dp[4][10-3]=11+6 得出来的，我们可以用10-3 走到了dp[4][7],
dp[4][7] 11 == dp[3][7] 所以物品4没有放入背包。然后走到了dp[3][7],
dp[3][7] 11 != dp[2][7] 9 , 所以物品3放入背包, dp[2][7-4] + 3 = 9 . 然后走到了 dp[2[3]
dp[2][3] == dp[1][3] ==6,所以物品2没有放入背包, 然后走到了 dp[1][3]
dp[1][3] != dp[0][3] 说明物品1放入背包，dp[0][3-2] + 6 , 然后就走到了dp[0][1].

and then will impement above code

fun knap01(): Int {

    val weightArr = arrayOf(1, 3, 4)
    val valueArr = arrayOf(15, 20, 30)

    val n = 5 // the number of goods
    val w = 8// the max of bag weight
    val dp = Array(n + 1) { IntArray(w + 1) } // 0 is nothing , so need one more

    //即dp[i][j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。
    //初始化

    //j==0 , 背包容量为0，放物品
    for (i in 1 until n) { //number
        dp[i][0] = 0
    }

    // i==0 nothing to put in bag
    for (j in 1 until w) { //weights
        dp[0][j] = 0
    }

    for (i in 0 until n) { //number
        // i==0 , nothing to put in bag
        for (j in 0 until w) { //weights
            if (weightArr[i] > j) { // 物品重量大于 背包容量
                dp[i][j] = dp[i - 1][j]   // if object weight < j , then use top item
            } else {
                dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weightArr[i]] + valueArr[i])
            }
        }
    }


 //这个需要后续的真题验证 
    val addedList = ArrayList<Int>()
    var j = w
    for (i in n downTo 0) {
        if (dp[i - 1][j] >= dp[i][j]) {
            j-=weightArr[j]
        }
    }
    return dp[n][w]
}

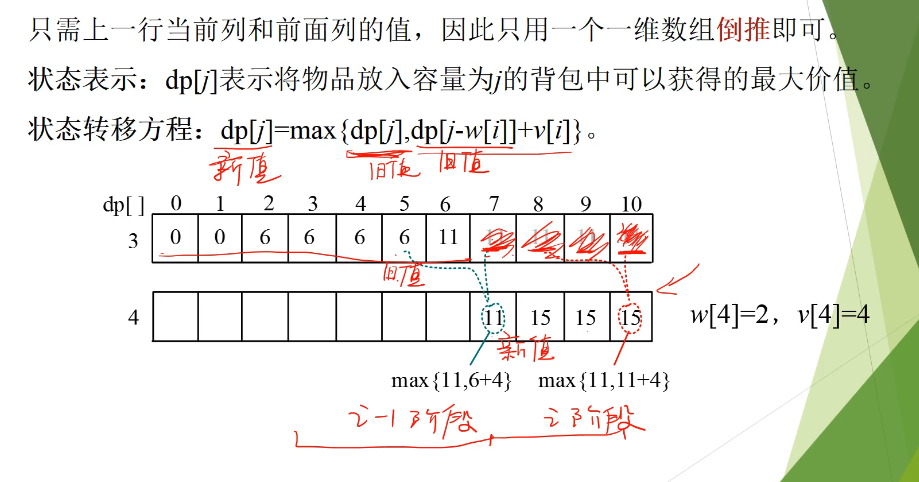
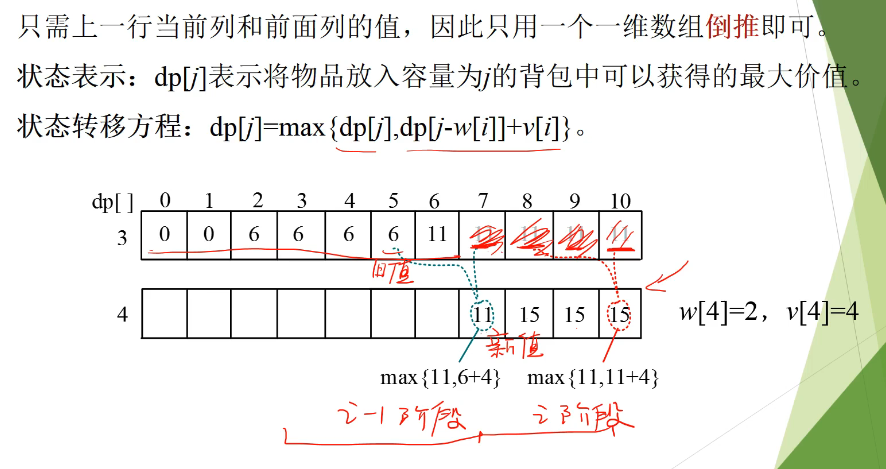
滑动数组

https://www.bilibili.com/video/BV1jT4y1o71J/

40:00

the video clearly talking about 01 knapstack problem which two ways.

Screenshot 2023-09-23 at 18.51.53.png

Screenshot 2023-09-23 at 18.50.37.png

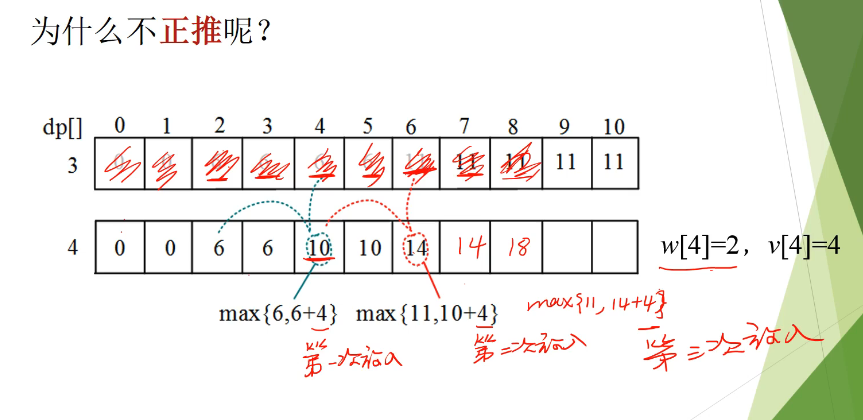
Screenshot 2023-09-23 at 19.04.19.png

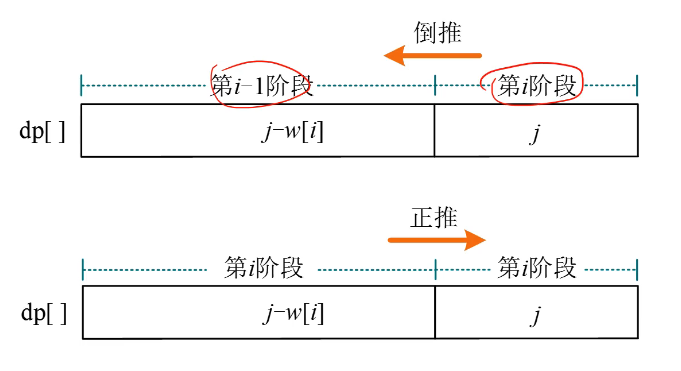
正推的时候，是拿着新值，去更新,新的值。所以第4个数会放入多次。

完全背包

1 - i 种物品可以取 n 次。

完全背包就是01背包

Screenshot 2023-09-23 at 19.18.50.png

这个代码需要验证

fun knapStackarray(N: Int, W: Int) {
    val weightArr = arrayOf(1, 3, 4)
    val valueArr = arrayOf(15, 20, 30)

    val dp = Array(4) { 0 }
    for (i in 1..N) {
        for (j in W downTo weightArr[i]) { // 只有j容量大于当前物品的容量，才会考虑添加到数组中，更新当前cell的值，否则就直接用上一层的值
            dp[j] = Math.max(dp[j],dp[j-weightArr[i]+valueArr[i]])
        }
    }
}

416. 分割等和子集

转化成背包问题的，1,5,11,5，背包容量11，前面题解是装到最大值但是不一定能装满，但是在这里不是拿到最大值，是装到最大值的情况,而且==11两个条件.刚好装满。

一开始打印的时候，发现超出了target,正常情况下是不可能的，加入放入新的物品后，留下的容量去之前的最大值去找，所以不可能超过.

fun canPartition(nums: IntArray): Boolean {
    var sum = 0
    nums.forEach {
        sum += it
    }
    if (sum % 2 != 0) {
        return false  // will not fill target exactly 
    }
    val target = sum / 2
    val dp = IntArray(target + 1)
    println("target $target")
    for (i in 0 until nums.size) {
        println()
        println("   i $i    ")
        println()
        for (j in target downTo nums[i]) {
            println(" j = $j   j - nums[i] = ${j - nums[i]}      dp[j - nums[i]]  ${dp[j - nums[i]]} ")
            dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]) // 一开始 dp[j] 写成了dp[target]排查了很久
            print("  dp[j] ${dp[j]}  ")
        }
        dp.printIntArray()
        println()
    }
    if (dp[target] == target) {
        return true
    }
    return false
}

1049. 最后一块石头的重量 II

两堆石头如果刚好一样大小，结果就是0，所以找出最接近中间重量的石头。

也就是转化成01背包问题了。

    fun lastStoneWeightII(stones: IntArray): Int {
        var sum = 0
        stones.forEach {
            sum += it // total sum
        }
        val target = sum / 2

        val dp = IntArray(target + 1)
        for (i in 0 until stones.size) {
            for (j in target downTo stones[i]) {
//                println(" j = $j   j - nums[i] = ${j - stones[i]}      dp[j - nums[i]]  ${dp[j - stones[i]]} ")
                dp[j] = Math.max(dp[j - stones[i]] + stones[i], dp[j])
//                print(" dp[j] ${dp[j]}  ")
            }
//            dp.printIntArray()
//            println()
        }
        return sum - dp[target]*2 // 这是target,而不是物品的size
    }

494.目标和

https://www.bilibili.com/video/BV16Y411v7Y6/?vd_source=d4c5260002405798a57476b318eccac9

花花酱 LeetCode 494. Target Sum 上 - 刷题找工作 EP156 - YouTube

12:00

positve 是正数的总和

negative 负数的总和

分析

positive - negative = target

positive + negative = sum

上面公式相加

positive = (target + sum)/2

然后就转化成 01背包问题 , 装满容量为positive的背包，有dp[positive]种方法。

确定递推公式

有哪些来源可以推出dp[j]呢？

只要搞到nums[i]，凑成dp[j]就有dp[j - nums[i]] 种方法。dp[j - nums[i]]，说明装进nums[i]后,剩下dp[j - nums[i]]的方法数, 一直往前找，初始dp[j]数组的值是0,

例如：dp[j]，j 为5，

已经有一个物品1（nums[i]）的话，有 dp[4]种方法凑成容量为5的背包。
已经有一个2（nums[i]）的话，有 dp[3]种方法凑成容量为5的背包。
已经有一个3（nums[i]）的话，有 dp[2]中方法凑成容量为5的背包
已经有一个4（nums[i]）的话，有 dp[1]中方法凑成容量为5的背包
已经有一个5 （nums[i]）的话，有 dp[0]中方法凑成容量为5的背包

那么凑整dp[5]有多少方法呢，也就是把所有的 dp[j - nums[i]] 累加起来。

所以求组合类问题的公式，都是类似这种：

1	dp[j] += dp[j - nums[i]]

这个公式在后面在讲解背包解决排列组合问题的时候还会用到！

//dp[j] += dp[j - nums[i]]对这句组合数的理解： 1、如果不选第i个数（nums[i]）的话，则方法数为dp[j]； 2、如果选第i个数（nums[i]）的话，则方法数为dp[j - nums[i]]；
// 所以方法总数为：dp[j] = dp[j] + dp[j - nums[i]]；（感觉这样拆开写比较容易理解）可以对比其他01背包问题：dp[j] = max(dp[j], dp[j - nums[i]])，这种问题即是从选i与不选i里，选取最大值。

fun findTargetSumWays(nums: IntArray, target: Int): Int {

      /**
       *  positive - negative = target
       *  positive + negative = sum
       *
       *  positive  =  (target + sum)/2
       *
       */

      //dp[j] += dp[j - nums[i]]对这句组合数的理解： 1、如果不选第i个数（nums[i]）的话，则方法数为dp[j]； 2、如果选第i个数（nums[i]）的话，则方法数为dp[j - nums[i]]；
      // 所以方法总数为：dp[j] = dp[j] + dp[j - nums[i]]；（感觉这样拆开写比较容易理解） 可以对比其他01背包问题：dp[j] = max(dp[j], dp[j - nums[i]])，这种问题即是从选i与不选i里，选取最大值。

      var sum = 0
      nums.forEach {
          sum += it
      }

      if (Math.abs(target)>sum) return 0 // 如果target 大于 sum是不可能有值的

      if ((target + sum) % 2 != 0) return 0 // positive 一定是正整数 ,这种情况下没有

      val positive = (target + sum) / 2
      val dp = IntArray(positive + 1)
      dp[0] = 1
      for (i in nums.indices) {
          for (j in positive downTo nums[i]) { // j表示背包容量
              println(" i = $i  j = $j   j - nums[i] = ${j - nums[i]}  dp[j - nums[i]]  ${dp[j - nums[i]]} ")
              dp[j] += dp[j - nums[i]]
              println(" dp[j] ${dp[j]}  ")
          }
          println()
          dp.printIntArray()
          println()
          println()
      }
      return dp[positive]
  }

这个看了很多视频，还不是特别理解，

474.一和零

装满m个0,n个1 容器的背包，有哪些物品，其实就是01背包，只是装的物品是两个纬度。


    fun findMaxForm(strs: Array<String>, m: Int, n: Int): Int {
        val dp = Array(m + 1) { IntArray(n + 1) }

        strs.forEachIndexed { index, str ->
            var oneNum = 0  // 一开始放，外面，要在里面
            var zeroNum = 0
            str.forEach {
                if ('1' == it) {
                    oneNum++
                } else {
                    zeroNum++
                }
            }
            for (i in m downTo zeroNum) { //
                for (j in n downTo oneNum) {
//                    dp[i][j] = Math.max(dp[i][j], dp[m - i][n - j] + 1) // 错的写法
                    dp[i][j] = Math.max(dp[i][j], dp[i-zeroNum][j - oneNum] + 1)
                }
            }
        }
        return dp[m][n]
    }

#LEETCODE

LC_DP_BAG

https://noteforme.github.io/2023/08/09/LC-DP-BAG/

Author

Jon

Posted on

August 9, 2023

Licensed under

compose_layout Previous

LC-DP Next